The purpose of this post is to give a basic overview and intuition on differential equations. Afterwards, we will look at how these principles come into play in some of the best-performing generative modeling frameworks to date.

Differential Equation Basics

You should be familiar with the fundamentals of calculus. Two very common operations are differentiation and integration, which are inverses of each other. We may write something like:

This states two things:

1. $x$ is a function of $t$, i.e. we can write $x(t)$.
2. The derivative of the function $x$ with respect to $t$ is $2t$.

For the purpose of this article, you can think of $t$ as a point in time, and $x$ to be some kind of position or state. Now you might want to find out what form $x(t)$ takes. This is simple to do via basic integration to find the antiderivative (or indefinite integral):

Here, the $C$ appears because the derivative with respect to $t$ is 0, so any value of $C$ would lead to the same overall derivative. If we have certain expectations on our function $x$, for example that $x(0) = 0$, we can fix $C$ to a specific value; in this case, $C = 0$ would be required.

Of course, not all integrals are so simple to compute. For example, if $\frac{dx}{dt} = \exp(-t^2)$, there is no antiderivative that can be expressed via elementary functions. In such cases, we can at least approximate $x(t)$ for some $t$ via numerical methods. Other integrals may be possible to compute analytically, but require significantly more work than the simple example above.

Differential equations are specific integral problems that look like this:

Alternatively, it can sometimes be convenient to write

To be precise, this is a so-called ordinary differential equation (ODE): $x$ is a function of a single variable $t$. There are other kinds of differential equations (including ones relating higher derivatives), but the main thing is that the derivative of the function $x$ is a function of $x$ itself. Since this is quite abstract, let’s consider a concrete example:

This means that the derivative of the function is the function itself. It’s easy to come up with a solution here: Since the exponential function is its own derivative, $x(t) = C\exp(t)$ is a solution to this differential equation. In many cases, we consider an initial value problem, where $x(t_0) = x_0$ must be fulfilled. Solving this leads to a fixed value for $C$. For the exponential function above, this translates to $x_0 = C\exp(t_0)$, or $C = \frac{x_0}{\exp(t_0)}$.

Approximating a Solution

This was of course a very simple example. There are many special cases of differential equations that allow for direct computation of the solution. But in general, finding a solution for any given differential equation can be difficult or impossible. In this case, we can approximate a solution by discretization. This is not unlike approximating integrals via adding up small rectangles.

Intuition

Recall that the derivative of a function gives the rate of change at that point. For example, if $\frac{dx}{dt} = 2$, the function $x$ changes at a constant rate of 2 units per unit of time $t$ (e.g. seconds). Let’s say that $x(3) = 9$. What will be the value at $x(4)$? Clearly, it will be $x(4) = 11$, since the change per second is 2. In fact, if we know $x(t_0)$ for a single $t_0$, we can get $x(t)$ for any $t$ by multiplying the rate of change by the change in time, i.e. $2 \cdot (t - t_0)$.

Now, if $\frac{dx}{dt} = 2t$, the rate of change increases linearly with time, leading to quadratic growth of $x$. Now, if $x(3) = 9$, the rate of change here would be $2\cdot 3 = 6$. So $x(4) = 15$, right? However, the true solution is $x(t) = t^2$, so $x(4) = 16$. What went wrong? The issue is that we used the rate of change at $t=3$, and extrapolated it to a larger range of time. But since the rate of change is variable, this is imprecise.

In fact, if we keep going, things will only get worse. If we assume $x(4) = 15$ is correct, and we want to go another step, we would arrive at $x(5) = 23$, since this is $15 + 2\cdot 4$: Our previous value at $t=4$ plus the rate of change at that time. We now have a difference of 2 to the actual value $x(5) = 25$. In fact, this will get worse and worse as we continue – the error accumulates.

Formal Definition

In general, given $\frac{dx}{dt} = f(x, t)$ and the initial value $x_0 = x(t_0)$, we can proceed as follows:

1. Define a step size $\Delta t$.
2. Compute the derivative at the current point, $f(x_0, t_0)$.
3. Define the change of $x$ as $\Delta x = f(x_0, t_0) \cdot \Delta t$.
4. Approximate $x(t_1) \approx x_0 + \Delta x$, with $t_1 = t_0 + \Delta t$.

This procedure can be repeated step by step, up to some desired $t_{max}$. You simply approximate the derivative over the range from $t$ to $t + \Delta t$ by the one evaluated at $t$, ignoring the fact that it will likely change over that range. Clearly:

• The error is worse for larger $\Delta t$.
• The error is worse the more curved $x$ is, with no error for linear functions.
• Errors will accumulate over time/iterations.

In terms of runtime, smaller $\Delta t$ requires more steps. Since each step has to be computed based on the previous one, this must be done sequentially. Thus, runtime increases in direct proportion to the inverse of the step size. This means that in practice, we have to find a good trade-off between runtime and accuracy.

The method outlined above is called the Euler method. This is a so-called first-order solver. Roughly, you can understand this as only relying only on the first derivative and not adapting to the curvature of the function. There are also higher-order methods – these usually involve some sort of “looking ahead” to try and correct for curvature. Such methods usually require multiple evaluations of the derivative to make a single step, but make up for this by achieving much lower discretization error. For example, a second-order solver can perfectly solve a quadratic function the same way Euler’s method can only solve linear functions. Thus, in practice you can often get away with far fewer steps for a higher-order solver, which means finding a solution at a given quality faster.

As an example, consider Heun’s method:

1. Define variables as with Euler’s method and compute $\Delta x$ and $x(t_1)$ (see above).
2. Compute the step from $x(t_1)$, i.e. $c = f(x_1, t_1) \cdot \Delta t$ (you might call $c$ a corrector).
3. Take the “real” step $x_0 + \frac{\Delta x + c}{2}$.

This means you are “correcting” the first-order step using information gained from the next time step.

Next, let us consider a “real world” example as illustration.

Cars! With Rockets!

Say you are building a toy car with a rocket engine. Of course you want to eventually have it drive around in the real world. But it’s probably a good idea to first simulate how the car will behave in different situations, rather than crashing it immediately. We can illustrate what might happen, using an image created by a generative model that probably uses some kind of differential equation in the background:

Let’s consider a number of iterations on our rocket engine, all of which will lead to different behaviors. In all cases, we will know the velocity of our car, i.e. $\frac{dx}{dt}$, and want to find out what is position over time will be, i.e. $x(t)$ (expressed in meters). We assume that the engine turns on at $t=0$, and the car starts at the initial position $x(0) = 0$.

Case 1: Constant Speed

Say our rocket engine, once started, instantly accelerates our car to a speed of 1, and it stays at that speed forever. Thus, $\frac{dx}{dt} = 1$ for all $t$. The solution is simply $x(t) = t$, i.e. after $t$ seconds our car will have travelled $t$ meters. We could also get an exact solution via Euler’s method sketched in the previous section. In fact, it doesn’t even matter how large the discretization step $\Delta t$ is – we can instantly jump to any desired $t$ simply by following the derivative, without knowing the functional form of $x(t)$.

Case 2: Burst of Speed

To have something slightly more interesting, say the rocket instantly accelerates the car to a speed of 1, but then fizzles out, leading to the car slowing down due to factors like friction and air resistance. Let’s set $\frac{dx}{dt} = \frac{1}{t + 1}$.¹ Solving this integral requires a slightly better grasp on calculus, but is still easy: $x(t) = \log(t + 1)$. The car will slow down to a crawl over time, but it will actually never stop, since the logarithm keeps growing forever.

We can once again try Euler’s method. This time, we can see the influence of $\Delta t$: The larger it is, the more we deviate from the true solution. In fact, we require around one hundred steps per second to achieve a good fit. Unfortunately, Euler’s method is not very usable in practice: $\frac{dx}{dt}$ may be expensive to evaluate, in which case the number of steps required makes it prohibitively slow. Let’s look another example, along with a better approximation method:

Case 3: Wind Tunnel

The two examples above are not “real” differential equations in that the derivative is not dependent on the function itself. We just computed some integrals. Let’s build upon Case 2, but say the car is in a wind tunnel, with a current blowing against it that becomes stronger as it moves forward. A very simple model could be $\frac{dx}{dt} = \frac{1}{t + 1} - \frac{x}{10}$. This means the wind becomes stronger in a linear fashion as the car moves forward, and as the rocket boost becomes weaker, it will eventually push the car back.²

This problem has suddenly become much more difficult. We need a function $x(t)$ such that its derivative is the negative of itself divided by 10, plus $\frac{1}{t+1}$. Solving such a differential equation requires special methods that go beyond the point of this article. But this can be solved (e.g. using Wolfram Alpha) to be

where $\mathrm{Ei}$ is the exponential integral.³ Below, we once again show a curve of the solution along with Euler’s method for various $\Delta t$. This time, we also showcase a second-order Heun solver.

We can see that the second-order method with $\Delta t = 1$ matches the first-order solution with $\Delta t = 0.1$. Since the second-order method requires two evaluations per step, this implies a 5x speedup for a similar solution quality! Going down to $\Delta t = 0.1$ with a second-order method gives a very good match with the true solution, save for slight deviations at the start.

There are higher than second-order solvers, as well. You can read up on the general family of Runge-Kutta methods, if you wish. However, we will now consider what happens when you add a random component to a differential equation.

Stochastic Differential Equations

The differential equations we have considered so far are fully deterministic. However, as we have discussed previously, many real-world processes are so complex to model as to be essentially random. For example, consider our rocket car in the wind tunnel: It’s unlikely that the force of the wind is perfectly consistent. Rather, the turbulent movement likely induces a somewhat “random” force at each point in time and space. Aside from that, stochasticity also plays an important part in generative models. As such, it may be useful to have some sort of stochastic analogue of ordinary differential equations. We will not treat this in any theoretical detail, but the major results here come from Itô calculus. As a stochastic differential equation (SDE), we can understand an equation of the form:

Here, $f(x, t)$ is called the drift, and $g(t)$ the diffusion coefficient. $dw$ is the so-called Wiener process. This is essentially infinitesimal Gaussian noise. Crucially, when you discretize the SDE and take a step of size $\Delta t$, this will add Gaussian noise with mean 0 and variance $\Delta t$.

To illustrate what an SDE might look like, say we update our wind tunnel example as follows:

Here, $f(x, t)$ is as before, and $g(t)$ is a constant. Clearly, we cannot “solve” this SDE in a classical sense, as due to the random component, there is no longer any fixed value $x(t)$. Rather, we would now have to consider probability distributions $p_t(x)$. That is, given some initial value $x_0 = x(0)$, for each $t$ we have a distribution $p_t(x \mid x_0)$, which gives the probability that the initial value $x_0$ is mapped to a specific value at time $t$. But the value at $t=0$ could also be random, $x_0 \sim p_0(x)$.

However, we will not concern ourselves with how to solve SDEs, i.e. how to find $p_t$. Discretization is still easy, albeit non-deterministic. Here are examples of several runs of the above SDE at $\Delta t = 0.01$ with different choices for $\sigma$. For each choice, we do 100 runs, each of which is represented by one line.

The results are as can be expected: For small noise levels, the runs are fairly consistent. The larger the noise, the more chaotic it becomes. Interestingly, the randomness seems worse later in the run, with early values being relatively more consistent. There are likely two reasons for this:

1. Specific to our SDE, $f(x, t)$ tends to be larger at the start, meaning it is more impactful compared to the constant diffusion coefficient. At later steps, the drift becomes weaker, meaning that the random component has a stronger influence on the movement.
2. In general, the random deviations accumulate over time and push $x(t)$ “off course” to different positions, which will lead to each run experiencing different drift values, and this in turn changes the trajectory of each run on top of the random noise component.

We will leave it at this high-level look at SDEs in general. Rather, we now turn to how they can be used for generative modeling.

From Score Matching to SDEs

Note: This section heavily relies on the original paper by Yang Song et al.

Recall (or see the papers if you need a refresher) that both score-based and diffusion generative models work by learning to reverse a “diffusion process” that turns data into noise. Since this process is somewhat simpler for classic score-based models, we will consider those first. We define a sequence of geometrically increasing noise levels $\sigma_t,\ t=1, \ldots, T$. Then, given some data $x_0$, we have $x_t = x_0 + \sigma_t\epsilon$, where $\epsilon \sim \mathcal{N}(0, 1)$ is a standard Gaussian sample. This way, we can get a sequence of $x_t,\ t=1,\ldots\,T$, and clearly, $p(x_t \mid x_0) = \mathcal{N}(\mu = x_0, \sigma^2 = \sigma_t^2)$, i.e. $x_t$ is a Gaussian around $x_0$, and with the corresponding variance.

However, each $x_t$ is just defined in terms of the original $x_0$. While this is practical, as we can just jump directly to any desired $t$, this does not build a good connection to SDEs, as these are defined in the change in $x$ from one step to the next. However, we can write an equivalent formulation as $x_t = x_{t-1} + \sqrt{\sigma_t^2 - \sigma_{t-1}^2}\epsilon$.⁴ Note that this is a Markov chain – each sample only depends on the previous one! Another way of writing this is $\Delta x = x_t - x_{t-1} = \sqrt{\sigma_t^2 - \sigma_{t-1}^2}\epsilon$. This gives the change between successive values $x_t$.

Now, for score-based models, we usually define $\sigma_1 = \sigma_{min}$ to be a very small value, such as 0.01 for images in range [0, 1], and some $\sigma_{T} = \sigma_{max}$ that is large enough to “drown the data in noise”. These values are fixed independent of how large $T$ is. Thus, if we increase the number of noise levels $T$, successive levels have to move closer together, as illustrated below:

Let’s make a small change to the notation. The indices we have chosen are clearly arbitrary. We could just redefine $\sigma_T \rightarrow \sigma(1)$, and $\sigma_t \rightarrow \sigma\left(\frac{t}{T}\right)$. All we did was fix $T \rightarrow 1$, and “squeeze” the other indices into the range [0, 1], accordingly. We also changed notation from indices to function values. But mathematically, nothing has changed! However, this prepares us for the next step.

Now imagine what happens if we were to increase $T$ to infinity, that is, if we kept adding more noise levels to the point that we have infinitely many. Because $\sigma_{min}$ and $\sigma_{max}$ remain fixed, the infinitely many noise levels have to squeeze into a fixed-size space, meaning that successive noise levels have to be infinitely close together. At this point, we have moved from discrete noise levels to a continuous space, with $t$ taken from a “time” interval [0, 1].⁵ Now:

• $x$ and $\sigma$ become functions of $t$ instead of discrete sequences.
• The difference between successive values of $x$, $\Delta x$, becomes a derivative $dx$.
• The difference between successive values of $\sigma^2$ also becomes a derivative: $\sqrt{\sigma_t^2 - \sigma_{t-1}^2} \rightarrow \sqrt{\frac{d\sigma^2(t)}{dt}}$
• The standard Gaussian noise $\epsilon$ becomes infinitesimally small – a Wiener process $dw$.

Thus, we have arrived at an SDE:

Here, $g(t) = \sqrt{\frac{d\sigma^2(t)}{dt}}$ and $f(x, t) = 0$.

For $\sigma(t)$, we can choose the following exponential function to mirror the usual geometrically increasing sequence:

And then we can solve:

which we can use as a concrete choice for $g(t)$. Because this process leads to a continuously growing variance, this is called the variance exploding or VE SDE. Finally, we have arrived at an SDE that we can use to turn our data into noise. In fact, you can show that $p_t(x \mid x_0) = \mathcal{N}(x_0, \sigma^2(t))$, so this is an exact analogue to the original discrete process. But what about a generative model?

Sampling via the Reverse SDE

It turns out, for the general SDE formulation of $dx = f(x, t)dt + g(t)dw$, a reverse can be found with relative ease:

Here, $dt$ is a negative time step. Crucially, this reverse SDE contains the score $\nabla_x \log p_t(x)$. The other components are already known from the forward SDE. This gives us a basic recipe for training and sampling a score model based on SDEs:

1. Training (for each step):
   • Sample $t \in [0, 1]$.
   • Given data $x_0$, sample $x_t \sim p_t(x \mid x_0)$.
   • Perform a standard score matching training step using $x_0$, $x_t$, and our model.
2. Sampling:
   • Start with a random sample $x_1 \sim \mathcal{N}(0, \sigma_{max}^2)$, which approximates $p_1(x)$.
   • Run the reverse SDE using the trained score model and a solver of your choice.

The second point for training corresponds to running the forward SDE up to time $t$, but for most practical cases you can actually compute $p_t$ directly, without iteration, which makes training very efficient, just as with standard score-based or diffusion models.

The SDE perspective opens up various paths for improving on “standard” denoising score matching models. Due to the length of this article, we only briefly discuss a couple here.

Diffusion Models as SDEs

Although they look somewhat different on the surface, DDPMs can be expressed in the exact same format. Here we have the diffusion process $x_t = \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon$. Again, $x_0$ is the original data, and this process always converges to a standard normal distribution, as long as the noise schedule $\beta_t$ is chosen appropriately. If we decide to use “infinitely many” noise levels, where each step becomes infinitely small, we again end up with a continuous process, namely $dx = -\frac{1}{2}\beta(t)xdt + \sqrt{\beta(t)}dw$. Thus, we have an SDE with drift $f(x, t) = -\frac{1}{2}\beta(t)x$ and diffusion $g(t) = \sqrt{\beta(t)}$, which is called the variance preserving or VP SDE.

In fact, you can show that diffusion models perform score matching even without the SDE connection. This can be exposed by rewriting the respective training algorithms somewhat, meaning that these models are already trained to output scores for noisy data. This, in turn, means we can use them for sampling via the reverse SDE.

New Model Types

Different choices for $f(x,t)$ and $g(t)$ can lead to new models. Of course, not all choices for these functions will make sense. However, the paper showcases one new SDE that is inspired by diffusion models, but adds noise less slowly, termed the subVP SDE, which tends to perform very well.

New Sampling Algorithms

Since we generally cannot solve these complex reverse SDEs in closed form, we have to employ discrete sampling methods. As previously discussed, the most basic method for ODEs is the Euler method. There is an analogue for SDEs called Euler-Maruyama. This is basically the Euler method, but incorporating random normal noise from the discretization of the Wiener process. This method is extremely general, and can easily be applied to any discretization of any SDE. In fact, it’s what we used for the “turbulent wind tunnel” example further above.

However, we can also make use of our knowledge of the original discrete process. For example, recall that for discrete score-based models, $x_t = x_{t-1} + \sqrt{\sigma_t^2 - \sigma_{t-1}^2}\epsilon$. This means we can construct a discrete analogue of the diffusion coefficient $g(t)$:

Then, we can sample down from $x_T$ to $x_0$ in $T$ discrete steps. This differs from Euler-Maruyama in that we can use our knowledge of the current and next noise levels in the discrete chain, rather than just the instantaneous change in noise level, which is given by $g(t)$. We are basically constructing a “classic” score-based model after training on a continuous range of noise levels. This also means that we can choose the number of noise levels $T$ freely. The same procedure can be done for the VP SDE, restoring “classic” diffusion models, or the subVP SDE, as well.

The above is termed the reverse diffusion sampler in the paper. Other samplers discussed there include:

• Ancestral sampling as used for the original diffusion models, with a derivation included for score-based models, as well.
• Corrector samplers, which correspond to annealed Langevin dynamics, the sampling method originally used for score-based models.
• Predictor-corrector samplers, which combine an SDE discretization like reverse diffusion with corrector methods by using them alternatingly.

Finally, they also connect back to ordinary differential equations (ODEs). Remember that those are deterministic! The remainder of this article will focus on the ODE perspective, which has become very popular in recent years.

ODEs for Generative Modeling

Remember the forward SDE turning data into noise:

As it turns out, you can construct an ODE that has the same marginals. That is, given the data distribution $p_0(x)$, the diffused distribution $p_t(x)$ will be the same for any specific $t$, no matter if we use the SDE or the equivalent ODE. This means that if the SDE maps a data distribution to, say, a standard normal distribution, the equivalent ODE will do the same when considering the data distribution as a whole. Of course each individual sample will be treated differently, as the equations are different. This ODE is called the probability flow ODE and is given by

Note that this is the forward ODE turning data into noise; but an ODE is very easy to reverse by simply running time backwards. Thus, the reverse ODE is the exact same equation, but with negative $dt$. Compared to the reverse SDE given earlier, the Wiener process $dw$ has disappeared, and $g(t)$ has acquired a factor of $\frac{1}{2}$. Because this is a completely deterministic equation, if we start generating from a specific random noise point at $p_1$, we will always generate the same data point. This contrasts with SDEs, where the random component at each step will lead to different generations when starting from the same noise sample multiple times. Furthermore:

• The forward ODE is deterministic, meaning a data point from $p_0$ will always be mapped to the same noise point in $p_1$.
• Forward and backward equations are inverses of each other, meaning we can “encode-decode” data samples to noise and back again. Save for discretization error, the ODE is invertible!
• $p_1$ can act as a proper latent distribution, allowing for applications such as interpolating between samples.

Intuition on Stochastic vs Deterministic Transformations

At this point, you may wonder how it can even be possible that an SDE and an ODE can transform a given data distribution to the same noise distribution. We will illustrate this with a simple example.

Consider the task of transforming a standard normal distribution $p_0$ to a normal distribution $p_1$ with mean $\mu_1 = 0$ and variance $\sigma_1^2 = 4$. Formally, we are given $x_0 \sim \mathcal{N}(0, 1)$, and want to find a transformation $f$ such that $x_1 = f(x_0) \sim \mathcal{N}(0, 4)$. Let’s consider two options.

Option 1: Adding another random variable

The sum of two normal random variables also follows a normal distribution. The means and variances simply add up. We could define an auxilliary variable $x_a \sim \mathcal{N}(0, 3)$ and set $x_1 = x_0 + x_a$. Then, $\mu_1 = \mu_0 + \mu_a = 0$, and $\sigma_1^2 = \sigma_0^2 + \sigma_a^2 = 1 + 3 = 4$ as desired.

Option 2: Multiply by a constant

When a random variable is multiplied by a constant number, the variance is multiplied by the square of that constant, and the mean is multiplied by the constant. This means we can set $x_1 = 2x_0$. Then, $\sigma_1^2 = 2^2 \sigma_0^2 = 4$. Also, the mean $\mu_1 = 2\mu_0 = 0$.

It seems like both options work: $x_1$ has the desired distribution in either case. However, the methods differ significantly. The first option is stochastic: If we were to take the same sample $x_0$ and transform it to $x_1$ twice, we would most likely get different results, since a different random value $x_a$ is added each time. In contrast, the second option transforms any given sample in th exact same way each time. This trivially implies that both methods will lead to different results when applied to a specific sample. And yet, when considering the distributions $p_0$ and $p_1$, both methods are the same! This shows that stochastic and deterministic transformations can be equivalent when considering distributions as a whole.

Below, you can see a graphic comparing both options empirically. On the left is $p_0$, on the right $p_1$. Top is the stochastic transform, bottom the deterministic one. For each, we also highlighted some specific points. For the stochastic one, we transform each “source” point multiple times, and we can see how the results differ. There is a vague relation between original and transformed points – the red point is originally somewhat higher up, and the transformations tend to be higher, as well. But this is not guaranteed. In contrast, for the deterministic transformation, the shape of the distribution is preserved exactly, as are relations between the different samples. However, the overall distributions look similar between the two cases.

Other Differential Equation Formulations

To close out this article, we will look at some more recent advancements in the field.

Modern Diffusion Models

First off, you may come across slightly different SDE/ODE formulations than the one we have seen so far. An influential paper by Tero Karras et al. formulates SDEs directly in terms of the $p_t$ they induce. Recall that we start with a data distribution $p_0$, and data $x_0$ is transformed (“diffused”) by the forward SDE to $x_t \sim p_t(x \mid x_0)$. However, the form of $p_t$ has to be inferred from the drift and diffusion coefficients, $f(x, t)$ and $g(t)$.

The authors propose to completely remove these coefficients, and instead work directly with an input scaling $s(t)$ and a noise schedule $\sigma(t)$, such that $p_t(x \mid x_0) = \mathcal{N}\left(s(t)x_0, \sigma^2(t)\right)$. This allows us to see directly how the input is scaled and how much noise is added at each time $t$, which should also make it easier to design new schedules. The authors then rewrite the actual ODE/SDE used for sampling in terms of the functions $s(t)$ and $\sigma(t)$. See the paper for details. In particular, equation 81 gives the full ODE.

Flow Matching

The above formulation still leads to a somewhat restricted class of functions. Even if you set $s(t) = 1$, corresponding to the VE SDE (as they do in the paper), you get

where $\dot{\sigma}$ denotes the derivative of $\sigma$. This means that the ODE has to involve the product between a function and its own derivative.

The authors of the Flow Matching technique instead propose to think directly in term of probability paths, which is just the collection of the diffused distributions $p_t$ for all $t$. That is, we ask “what is the path we want to take from $p_t$ to $p_{t’}$?” Unfortunately, the terminology and notation in the paper is quite different from what we have considered so far, making it somewhat difficult to understand. But they connect back to flow models, specifically continuous normalizing flows. In what follows, we will be adapting some of the notation to be more similar with the rest of this article.

Basic Description

Recall that in flows, we want to transform a simple distribution $p_0$ into the data distribution $p_1$ (unfortunately, this is reversed from the SDE literature) via a series of invertible transformations. These transformations often only make a small change to the input. Consider what would happen if we added more and more layers to the flow. Since $p_0$ and $p_1$ are fixed, each layer would have to make a smaller and smaller change. In the limit, you have infinitely many layers making infinitely small changes – a continuous process! Since flows compute deterministic functions, this is an ODE:

That’s it! You can imagine $v_t$ being a neural network that directly outputs the change in $x$ (“velocity”), rather than a score function. Integrating this velocity over $t$ then defines a flow $\psi_t(x)$. Instead of having many “flow layers”, we have one function that is dependent on $t$ (the “depth” of the layer). The ODE form also means this flow is trivially invertible (save for discretization error).

$v_t(x)$ can be understood to mean the same as $v(x, t)$. Flows are trained by mapping the data back to the simple distribution $p_0$, and maximizing the probability there. Unfortunately, this requires running the full ODE for each training step, which is very slow. Flow Matching improves this by deriving a training recipe that works at single time steps. We will not discuss details here, but at a high level, this is it:

• Define a conditional flow $\psi_t(x_0 \mid x_1)$ that determines how a noise sample $x_0$ is transformed to a data sample $x_1$.
• Figure out the correct conditional vector field $u_t(x \mid x_1)$ such that $d\psi_t(x_0 \mid x_1) = u_t(\psi(x_0 \mid x_1) \mid x_1)dt$, i.e. $u$ is the derivative of $\psi$. ⁶ By construction of the flow, $u$ will point towards $x_1$.
• Train the neural network $v_t(x)$ to match $u_t(x \mid x_1)$ along the entire trajectory of $t$, for noisy inputs $x \sim p_t(x \mid x_1)$.
  • $p_t(x \mid x_1)$ can be sampled by sampling random $x_0 \sim \mathcal{N}(0, 1)$ and applying $\psi_t(x_0 \mid x_1)$.

Roughly speaking, the network has to figure out the direction towards the clean data $x_1$ from the noisy input $x \sim p_t(x \mid x_1)$. After training succeeds, we can then take a random sample from $p_0$ and follow the direction given by the neural network output. In practice, we are discretizing an ODE!

Intermezzo: Conditional Probability Paths & Score Matching

The fact that we are using conditional flows and vector fields is crucial for Flow Matching to work in practice. Let’s think back to score matching models. The goal is to learn the score $\nabla_x \log p_t(x)$ for the noisy distributions $p_t$. However, we don’t actually have access to these distributions, as they depend on the unknown data distribution $p_0$. Instead, we only ever work with the conditional distributions $p_t(x \mid x_0)$, i.e. putting noise onto specific data samples $x_0$. For these distributions, we can easily know the functional form (e.g. a Gaussian centered around the data point), which gives us a properly defined target for training.

The “magic” of denoising score matching is that matching the conditional scores also leads to the model learning the marginal scores in expectation, but this is not trivial! The same can be derived for Flow Matching, which is likely also where the name comes from: Matching the conditional vector fields of the conditional flows will also lead to matching the marginal vector field corresponding to the desired probability path.

Flow Matching in Practice

The given ODE format allows for more flexibility in the choice of probability paths. The authors consider a general form of affine flows:

If $x_0$ is initially drawn from $\mathcal{N}(0, 1)$, this results in a distribution $p_t(x | x_1) = \mathcal{N}(\mu_t(x_1), \sigma_t^2(x_1))$. As long as $\mu_1(x_1) \approx x_1$ and $\sigma_1(x_1) \approx 0$, the flow will always “end” in the data $x_1$.

Specifically, the authors propose to use a flow that simply computes a linear interpolation between noise and data:

Then, $u$ evaluated at the flow output is just the derivative with respect to $t$:

This is simply the difference vector between original data and random noise, and it’s the same for all $t$! The network $v_t$ will receive the partially noisy input $\psi_t(x_0 \mid x_1)$, and try to match the target velocity $u_t$.

This setup is ideal in the sense of optimal transport (OT). Roughly, this leads to the path between noise and data being perfectly straight, and move at a constant speed. However, this only holds for the conditional flow given a real data sample $x_1$, and not necessarily for the actual sampling trajectory starting from pure noise. The framework also allows for different paths: For example, ODEs corresponding to the VE/VP/subVP SDEs considered previously can also be derived. Still, the main attraction is the OT path, which is supposed to lead to faster and more stable training, and allow for sampling with fewer steps. This makes sense: The more linear (“straight”) the path, the less discretization error we obtain with a given number of steps. A perfectly straight path could be sampled with no error via a single Euler step.

Other Recent Models

Finally, we mention related frameworks for constructing generative models with ODEs. Rectified Flows are extremely similar to Flow Matching. They also introduce the idea of reflow, where you train multiple models in sequence, which are supposed to successively straighten the probability paths, to the point that you can eventually get respectable results via a single sampling step, jumping directly from $x_0$ to $x_1$.

Consistency Models are trained to produce the same output from any point along the ODE path, with the output for the data $x_0$ (yes, we are switching again…) being forced to be $x_0$ itself. This eventually results in the model learning to output clean data $x_0$, no matter the noise level of the input. In the best case, this can also allow for single-step sampling.

Conclusion

We can actually tie back the discussion to the initial “rocket car” example, but now the situation is a little different. You want to go from $a$ to $b$, and have to build the best engine to get there reliably. Initial attempts were mostly concerned with getting there at all. No we are entering the phase where it’s all about getting there quickly and reliably, and stopping at the appropriate place. What kind of engine seems to be the best: One that starts quickly, then slows to a crawl? One that speeds up in an exponential fashion? Or one that just moves at a constant speed? You decide. ;)

Using differential equations for generative modeling is a very active and complex field. This article only gave a brief look at the basics and some current models. The unfortunate reality is that this field is mathematically challenging, fast-moving, and uses inconsistent terminology. As such, really getting into it requires a lot of work. We hope that you could at least obtain a basic understanding of the concepts involved. A deep appreciation of the finer details will require sitting down and implementing and tinkering with these models yourself. Have fun!

This post assumes familiarity with VAEs, although the details of that framework are actually not super important to understand the topics discussed here. It also gets quite technical about minor details. If you are reading this because you have been following our LGM class, consider this advanced optional reading for those interested in mathematical details.

Reconstruction Loss in Variational Autoencoders

Recall that we would like to maximize the log probability of the data, $\log(p(x))$, but this is intractable in most latent variable models. Thus, we optimize the variational lower bound instead:

Here, the left term is the Kullback-Leibler-Divergence between the variational posterior and the prior, and the right part is the log-likelihood of the data. In this article, we want to focus on the latter part.

We have previously seen how to convert abstract probabilities into concrete loss functions we can then optimize. The main step, as before, is to find a suitable distribution $p(x|z)$. There is just one challenge: Previously, we dealt with $x$ just being a single number. But in the case of VAEs, we usually deal with high-dimensional data such as images consisting of many pixels. That is, one datapoint $x_i$ in our dataset is actually a vector of numbers, $x_i = (x_{i1}, x_{i2}, \ldots, x_{id})$ for images with $d$ pixels.¹ Accordingly, we need high-dimensional probability distributions over vectors. These can often be complex to evaluate, which in turn makes optimization difficult.

The Independence Assumption

There is one way to side-step the above issue: For two random variables $a$ and $b$, if they are independent from each other, then $p(a, b) = p(a)p(b)$, meaning that the joint probability factorizes. For our image-pixel example, that would mean for an image $x_i$,

Or in the log case:

This means that, if we assume independence between pixels given $z$, the (log-)likelihood decomposes into probabilities for each single pixel. And that, in turn, means we can once again focus on probability distributions over just single numbers.

However, you may ask if this assumption makes sense. Intuitively, assuming independence between pixels just seems wrong. In natural images, clearly there are dependencies between different positions. For example, neighbouring pixels tend to be of similar color. There may also be longer-range dependencies, such as in repetitive patterns across an image. However, note that we only require independence given $z$. You can imagine this to mean that the latent variables $z$ are responsible for “coordinating” the distributions over the different pixel positions, such that neighboring pixels are likely to match anyway. Still, the assumption is likely problematic – but it’s also the easiest solution by far.

Choosing a Distribution

In our previous examples, the choice of distribution for our data was relatively straightforward. In the coin flip example, the Bernoulli distribution was a natural choice. In linear regression, the assumption of a Gaussian-distributed error term lead to a Gaussian distribution on $y$, as well. But for image pixels, there seems to be no natural choice. Maybe we just pick something and see what happens?

Gaussian, Fixed Variance

We could just go with a Gaussian again. Does this make sense? Not really: The Gaussian distribution is non-zero over the entire range of real numbers, meaning that for a Gaussian-distributed random variable, technically any value should be possible. Of course, anything more than a few standard deviations away from the mean is near-impossible in practice, so we can often get away with assuming Gaussians where they are technically “wrong”.

But what about the image case? Most often, we represent pixels as being in the range [0, 1]. This is a quite narrow range. What if we want to represent the belief that a certain pixel should be black (represented by the number 0), with a slight chance of being somewhat lighter? We might predict a mean of 0 and assume a small standard deviation. But that would automatically extend our distribution into the negative numbers, since the Gaussian distribution is symmetric.

Still, the practical relevance of this issue is a bit questionable, as we usually just use the mean anyway, and we can easily restrict that into a range either through clipping or a squashing function like the logistic sigmoid. For now, we could just see what happens. In fact, this is exactly the same situation as with the regression model we considered in the last article: Maximizing a Gaussian likelihood with fixed variance is equivalent to minimizing the mean squared error. Thus, if you make the following assumptions:

• Pixel values are independent given $z$,
• Pixels follow a Gaussian distributions with a “global” fixed variance,

then the mean squared error is the correct reconstruction loss for our VAE. Still, it can be instructive to consider other choices.

Bernoulli

If you go and look for VAE code tutorials on the web, you will find many that use the binary (or sigmoid) cross-entropy, among them the official Tensorflow VAE tutorial. Recall from the first post in this series that the binary cross-entropy is what you get as a loss function when assuming a Bernoulli likelihood and apply maximum likelihood:

The Bernoulli likelihood is intended only for binary $x \in {0, 1}$. However, the formula above works perfectly fine for any $x$ in the range $[0, 1]$. Below is a graph of the cross-entropy as a function of $\theta$ (our model output) for various values of $x$ (the data):

It’s not so easy to see on the graph, but for each $x$, the minimum of the function is at $\theta = x$, and so using this as a reconstruction loss should lead to proper results: It is minimized if and only if the output is equal to the data. And yet, from a probabilistic perspective, this whole thing makes no sense. If our data consists of real numbers in a range, it cannot be Bernoulli-distributed. And simply extending the Bernoulli distribution from binary numbers to the whole range $[0, 1]$ does not result in a probability distribution – it does not integrate to 1. As such, using the cross-entropy for non-binary data is technically invalid.

It looks as though we haven’t really found the ideal reconstruction loss yet. The Gaussian assumption is clearly violated for images, and the assumption of one fixed variance for the entire dataset and all pixels in an image is also questionable. And the Bernoulli assumption is simply invalid. In the remainder of this article, we will look at some attempts to fix these issues. Be warned: This will get quite deep into the nitty-gritty of various probability distributions and should be considered an advanced topic.

Can We Fix It?

Continuous Bernoulli

It seems that we just need a probability distribution defined over the range $[0, 1]$. Then we can derive the log-likelihood and use that for our reconstruction loss. The paper The continuous Bernoulli: Fixing a pervasive error in variational autoencoders does just that. The idea is straightforward: We keep the form of the Bernoulli distribution, but normalize it such that it integrates to 1. This can be achieved by computing the integral over the Bernoulli distribution and then simply dividing by it. The paper claims improved results over the Bernoulli distribution, as well as other valid distributions such as Beta or truncated Gaussian.

Let’s investigate this distribution more closely. Since the continuous Bernoulli (CB) distribution is just Bernoulli multiplied by a normalizer, the log-probability is simply the log-Bernoulli plus the log-normalizer:

The form of the normalizer $C(\theta)$ is given in the paper linked above, so please refer to that for details. We can plot the log-normalizer and the log-probability for various parameters $\theta$, and compare it to the incorrectly applied “log-probability” of the standard Bernoulli distribution (see above):

As we can see, the log normalizer increases for the more extreme values of $\theta$. This should push the parameter more towards those values, compared to the standard Bernoulli likelihood. However, for our reconstructions, we usually want to plot the expected values, not the distribution parameters – this is a crucial point we will discuss further below. For the common Bernoulli or Gaussian distributions the expected values are actually just $\theta$ and $\mu$, respectively. That is, they are identical to (one of) the distribution parameters. But for the CB distribution, this is not the case. Here is a plot mapping the distribution parameter $\theta$ to the expected value of the distribution:

As we can see, the expected value is always less “extreme” (i.e. further away from 0/1) than $\theta$. This means we actually need more extreme $\theta$ values to model any given data point, compared to the regular Bernoulli distribution. As such, this property of the CB distribution is neither good nor bad in itself. Instead, let’s look at some concrete examples to evaluate whether this distribution is actually a good choice.

Sharpness

In section 5.1 of the paper, the authors claim that CB results in sharper images. This would be great, as blurry outputs are a common issue with VAEs. They demonstrate this by plotting the distribution parameters output by the network, not the expected values. Below is a plot that shows how misleading this is. I trained a VAE on MNIST using the CB likelihood. On the left is an image from the dataset, in the middle the “reconstruction” using distribution parameters, and on the right the reconstruction using expected values.

We can see that the supposed sharpness advantage is no longer present when showing the expected values. In fact, the background looks grey instead of white! We will return to this specific issue in a moment. Now you might say, maybe plotting the parameters is just better? But here is the same for an autoencoder trained on CIFAR10:

Clearly, the middle image (parameter reconstruction) is extremely oversaturated, whereas the right (expected value reconstruction) seems fine. In the paper, the authors also report results for CIFAR10, but conveniently leave out any reconstruction plots. I find this very fishy, as those would have clearly shown the issue. To me, this raises the question whether the paper is intentionally misleading, or the authors didn’t properly analyse their own models. In fact, you can already see an “oversharpening” of sort in the MNIST image – the reconstruction using the parameter values look sharper than the original, which is not a good reconstruction.

Instability and Color Range

As we have seen above, plotting the distribution parameters as reconstructions is a bad idea. This leaves us with the expected values. However, recall the mapping between parameter and expected value we plotted further above. This function becomes extremely steep near the edge values 0 and 1. This means that, to get an expected value of, say, 0.9, our model needs to output a distribution parameter very close to 1. And what about an expected value of 1, which would be necessary in datasets like MNIST, or any RGB image containing white color? It turns out, this just doesn’t work. The steepness of the mapping means that even tiny changes in $\theta$ lead to huge differences in the expected value. In fact, the code provided by the authors actually cuts off $\theta$ near the edges, as values too close to 1 lead to numerical issues when trying to compute the expected value and log-normalizer. This means it is practically impossible for CB to output images with proper black or white colors. To give you some concrete examples:

• For $\theta=0.9999$ (default choice in the authors’ code), the expected value is merely $0.8915$.
• For $\theta=0.9999999$, the expected value is $0.9373$.
• For $\theta$ even larger, 32-bit numerics fail and we just get an expected value of $1.0$. Also, models trained with $\theta$ allowed to cross this range tend to diverge to infinite loss, since the log-normalizer becomes infinite (at 32-bit precision).

The situation near 0 is symmetric – we either get values nowhere near 0, or the result underflows to a small negative (!) number. This is why, in the plot further above, we see a grey background in the reconstruction, rather than a proper white one. This is no issue for a model trained with standard Bernoulli or Gaussian likelihoods, for example. Here is another example showing a CIFAR image with black & white elements, and the CB reconstruction:

The parameter reconstruction in the middle is overblown, while the expected value reconstruction on the right is too dark.

Comparing FIDs

So, subjective comparison doesn’t look good for the CB likelihood. For completion, I also ran some evaluations using the FID score. I trained simple VAEs on MNIST, keeping all details the same, except for Bernoulli vs. CB likelihood. FIDs were computed using a custom MNIST classifier rather than an Inception network. I also used the beta-VAE framework and tested a range of $\beta$ values. Here are the results:

We can see that the results are very similar when controlling for $\beta$. CB likelihood seems to be more robust to a wider range of values, and the best FID reached is actually slightly better than the best one for the Bernoulli likelihood. However, this may well be due to random deviations, as well as insufficient sampling of the $\beta$ space. The main takeaway is that CB likelihood seems to require larger $\beta$. This makes sense: Compared to Bernoulli, CB adds an additional term to the reconstruction loss, which should lead to larger gradients, and thus relatively less impact for the KL-divergence. This, in turn, requires larger $\beta$ to make the KL-divergence more important.

So are these two losses ultimately just “the same”? I would argue no, since the problem of de-saturated images for the CB likelihood remains. The fact that the FID (or the Inception Score, for that matter) doesn’t seem to pick up on this is more of a statement about the blind spots of such measures. At the end of the day, we seem to be left with a rather frustrating conclusion: We can blatantly ignore the limits of our probabilistic framework by using a completely invalid target function (Bernoulli likelihood on a range rather than binary numbers), and yet it seems to work just as well as a different target derived from actual mathematical principles (Continuous Bernoulli). Sometimes, practicality beats correctness.

Of course, we could also probe other distributions over the [0, 1] range, such as the Beta distribution. This one is interesting since it has two parameters $\alpha$ and $\beta$, which generally allows more control over the shape of the distribution. It also makes clear that plotting distribution parameters (as was done in the CB paper) makes no sense, since we have two values for every pixel in this case! The added flexibility can be seen by the fact that the same mean (given by $\frac{\alpha}{\alpha + \beta}$) can be achieved by infinitely many combinations of parameters, as long as the ratio stays the same. Yet, these distributions will have different variances: Generally, larger parameter values will result in smaller variances. This can allow a model to express a measure of “certainty” in the predictions, independent of the expected value. On the flipside, this can get numerically unstable in case of values that are 100% predictable (such as background pixels in MNIST), and requires a few tricks to keep from diverging. Maybe there are more straightforward options with two parameters…?

Revisiting the Gaussian likelihood

Recall the Gaussian log-likelihood:

Previously, we have assumed that $\sigma$ is constant, and after removing constant factors, we were left with the mean squared error. As stated earlier, by assuming conditional independence between pixels, we can then justify applying this loss per pixel. But does this really make sense? Consider a dataset like MNIST. Pixels around the edges are always 0, while others take on varying values. Shouldn’t the edge values be much easier to predict, and thus have a lower standard deviation? This indicates we may want to have a different $\sigma$ per pixel. Also, some images may be easier to predict in general than others, indicating different $\sigma$ values per image. And even if we ignore all that – the constant $\sigma$ assumption was previously useful because it removed the parameter completely from our equations. Does this still hold for VAEs? No!

Recall that for a VAE, we add the KL-divergence to the reconstruction loss, which in turn is the negative log-likelihood. As you can see above, the squared difference is scaled by $\sigma$. But the KL loss is not! This means that, if we just ignore $\sigma$, we are basically forcing a specific relative scale between reconstruction and KL losses. It is in fact similar to setting the $\beta$ value on the KL loss in $\beta$-VAEs. You can imagine it like this: By removing the multiplier $2\sigma^2$, we have basically assumed this value is 1. This implies $\sigma^2 = 0.5$ or $\sigma = \sqrt{0.5} \approx 0.7$. That is, our model assumes a fixed standard deviation of around 0.7 for all pixel predictions. Doesn’t this seem excessively large for values ranged between 0 and 1?

But it gets worse: Scaling images in [0, 1] seems arbitrary. What if we decided to scale them in [0, 255]? Suddenly, a standard deviation of 0.7 is tiny! Note that a smaller $\sigma$ corresponds to a larger squared error, which makes the reconstruction loss more important relative to the KL-loss. All this implies that, even if we are okay with $\sigma$ being a single constant value, at the very least we have to tune it properly. Let’s consider some options for treating $\sigma$. I also recommend the paper on $\sigma$-VAEs, where some of these ideas come from.

• Leave it as a single fixed value that we tune by hand. This is equivalent to $\beta$-VAE.
• Have one fixed value per data dimension (e.g. pixel). This adds flexibility, but seems practically infeasible. Nobody wants to set thousands (or millions) of $\sigma$ values per hand.
• Use either of the above options, but have $\sigma$ be a learnable parameter. By analyzing the log-likelihood, you can see that there are two opposing factors: Maximizing $-\log(\sigma)$ pushes $\sigma$ to be as small as possible. On the other hand, the squared error pushes $\sigma$ to be as large as possible. These two factors will “meet in the middle” somewhere, depending on the value of the squared error.
• Use either of the first two options, but compute $\sigma$ from the data.

All these options have in common that they will use the same $\sigma$ values for all data points (e.g. images). This is somewhat limiting: Remember that our model outputs a probability distribution per data point, so we could use different $\sigma$ values for each example! The most straightforward way is to have $\sigma$ be another output of our model, along with $\mu$. This is easy to implement, and can be trained via backpropagation just like the values for $\mu$. Once again, we can either output a single $\sigma$ per image, or one per data dimension (pixel). For making predictions, $\sigma$ can simply be discarded, and $\mu$ used as output as usual. Thus, adding $\sigma$ as another output only affects the computation of the loss.

Given that $\sigma$ is in some sense a “secondary” parameter (only used for training), we can even take another approach. Namely, we can ask ourselves what the best value for $\sigma$ would be given a specific prediction for $\mu$. Once again there are different cases, such as one $\sigma$ per image, or one per pixel. Let us first look at the latter case – one value per pixel, or generally per data dimension. Here is the full per-dimension loss, which is just the negative log-likelihood:

The left term can be discarded since it’s constant, leaving us with

To find the optimal value for $\sigma$, we can go the usual route: Compute the derivative, set to 0, and solve. the derivative is

Setting this to 0 and solving for $\sigma$ gives

So the optimal variance, is just the squared distance from the mean, which makes sense. Now we can insert this into the loss above to remove $\sigma$ from the equation:

It turns out, the terms on the right cancel out, since both are just the squared difference! We can of course remove the constant, leaving us just with $\log(|x-\mu|)$. For high-dimensional data such as images, we would simply compute this loss per-element and sum up, as we have seen in the beginning of this article. Here is a plot of this function:

There are a few things to note about this loss function. For one, since $\log(0) = -\infty$, this loss does not have a proper minimum. Rather, it will keep decreasing as the difference gets closer to 0, eventually becoming infinite. This is obviously a problem for actual implementations. In practice, we need to set a lower bound on the variance to prevent this. This loss also has the property that the gradients become larger as the difference gets closer to 0. Essentially, this means that the better a specific value is predicted, the stronger the “pull” will be to predict it even better. Intuitively, this corresponds to reducing the variance of the Gaussian to concentrate it more and more on one point (the mean), which will make it ever more “peaked” and increase the probabilities close to the mean. This property is somewhat opposite to the squared loss, where the gradient (and thus the pull towards a specific value) becomes smaller the closer you get to the target value.

Is this good or bad? I’m not sure. But I personally have not been able to train models with this loss function. It’s simply too unstable. As soon as just one pixel in an image can be predicted near-perfectly, the process seems to diverge, even with a lower bound on the variance. And this is a very simple condition to meet for datasets like MNIST with pixels that are always background.

We could look at a slightly different model, namely one where we have just one $\sigma$ for an entire image. Here, we cannot look at single-pixel losses individually, since $\sigma$ is shared over pixels. However, we can at least keep the assumption of independence between pixels. This implies a Multivariate Gaussian with diagonal covariance matrix. The likelihood looks like this:

Here, $x$ and $\mu$ are now entire vectors, and $||\cdot||^2_2$ denotes the squared euclidean norm, i.e. sum of squares. $d$ is the dimensionality of the data, e.g. number of pixels. Now, the steps are the same as before. Compute the negative log-likelihood and remove constants to get a loss function:

Compute the derivative with respect to $\sigma$:

Setting this to 0 and solving for $\sigma$ now gives

Since the numerator is the sum of squared differences from the mean, this is just the mean squared error! We end up in much the same situation as before, where the two terms on the right of the loss function cancel out, and we are left with

The expression in the logarithm is the “root mean squared error”. Some further simplification of these terms and removing constants gives us

$\frac{d}{2}$ is a constant, but recall that we need to keep multiplicative constants in VAEs to properly scale the reconstruction loss vs. the KL-Divergence. All in all, this loss is similar to the one where we used one $\sigma$ per data dimension. However, the logarithm is applied to the sum of squares, rather the dimension-wise absolute difference. This change makes for a much more stable loss, since we are less likely to have differences near 0 for an entire image, compared to just single values.

I have not tested this loss function extensively, but good pretty good results from small test on FashionMNIST. The property of gradients becoming stronger as predictions become better takes some getting used to, and I still needed to tune $\beta$ for the $\beta$-VAE framework, contrary to what the paper claims.

Conclusion

This was a long one. To summarize:

• We saw how to construct reconstruction losses for (variational) autoencoders by deciding on probability distributions for our data and following the same approaches we have seen in previous articles.
• We learned how assuming conditional independence between data dimensions leads to simple element-wise loss functions.
• Finally, we investigated the questionable assumptions behind commonly used loss functions, and looked at some potential remedies, such as the Continuous Bernoulli distribution, or modeling $\sigma$ in Gaussian distributions.

Unfortunately, it doesn’t look like there is a definite answer for what is the best loss function. Like so often, a paper introducing a new function somehow always shows that this is the best one, but trying to reproduce those results in different contexts is a different story. We have also seen that “incorrect” functions like the binary cross-entropy or squared error can lead to acceptable results.

Still, if we really want to understand generative models deeply, including the theory, these are topics we need to deal with. There doesn’t need to be a correct answer at all; what matters is that we learn how to find and investigate potential new solutions! I hope this mini-series was helpful in doing that. There may be more articles in the future on other topics related to our Generative Models class. See you there!

Linear Regression

In regression, we generally have some data for so-called independent variables $x$ and dependent variables $y$, with $y$ assumed to somehow depend on $x$. In linear regression, this dependency is assumed to be… linear:

To be precise, this is an affine-linear model: The input is multiplied by some weight $w$, resulting in the typical straight line, but the line can be shifted away from $(0, 0)$ by the bias $b$. As an example, let’s consider the relation between a person’s height $x$ and weight $y$. Clearly, taller people tend to be heavier on average. It’s not so important whether this relation is really linear – we will just assume that it is so we have an example.

So let’s say we assume a linear relationship, but we don’t know what exactly that relationship is. That is, we don’t know $w$ or $b$. Just like with our coin flip example, we can go and collect data – in this case, this would mean finding a bunch of people and measuring their height and weight. This gives us height data $X$ and weight data $Y$. Then we could define a loss function that measures the difference between model predictions and the true values, and minimize that function. Done! A suitable loss function may be the squared error. But why? Why not the absolute error? Why not some kind of cross-entropy measure? Or something completely different?

Also, the linear model clearly doesn’t explain everything: What about two people who are the same height, but different weight? Clearly, there are other factors at work, so our model cannot be correct. We could try and collect a host of other influences (such as age, gender, ethnicity, physical activity, nutrition…) and include all these in our model. This would significantly complicate the process. Or we once again fall back on abstraction!

Linear Regression With a Random Component

Just because there are other factors influencing weight besides height, that doesn’t mean the relationship between the two variables isn’t linear. We just need a way to conveniently summarize all these other influences. We can do this just like in our coin flip example – by assuming they are essentially random. This means the proper linear regression model is actually

where $\epsilon$ is a random variable that summarizes all the influences on weight besides height. To have a proper model, we still need to specify what distribution $\epsilon$ follows. By far the most common pick for linear regression is to say that $\epsilon$ follows a Gaussian (or Normal) distribution with mean 0 and some unknown but fixed standard deviation $\sigma$. We write $\epsilon \sim N(0, \sigma)$. In practice, this means that, if I collect tons of weight data for people of the same height, the distribution should be a Gaussian bell curve around some mean value.

Crucially, the assumption of a fixed $\sigma$ means that this bell curve should have the same spread for all heights. Whether this is true in our example is questionable, and it’s likely that linear regression has been applied to many problems without really checking for this assumption! To illustrate, consider the two plots below: On the left, the assumption of fixed variance is fulfilled. On the right, it’s not – the spread of the data differs along the x-axis.

Next, note that we can actually rewrite $y$ as a random variable:

This means that $y$ follows a normal distribution with mean $wx + b$. This formulation is equivalent to the one with adding a 0-centered $\epsilon$. Now we can see that this kind of linear regression is a probabilistic model!

You might say that this seems problematic, as we don’t want to make random predictions about our data. But we don’t have to! In practice, we usually just predict the mean, i.e. $wx + b$. You can actually justify this mathematically, as well. Namely, we want to make the best prediction given our model, and it turns out that the mean is in fact the best prediction under certain assumptions about what “best” means. For example, we might want our prediction to minimize the expected squared error between itself and the true (random) value.

Finding the Best Model

Crucially, the formulation as a probabilistic model gives us a principled way to approach finding the best parameters. Since we went through these steps for the coin flip example in the las post, we will not repeat them here. However, we can once again apply the maximum likelihood principle (or optionally add a prior).

The actual equations are slightly more complicated, because now we have both $X$ and $Y$ for data. Most importantly, we are no longer directly optimizing the parameters of our probability distribution, as we did with $\theta$ for the coin flip. Rather, the mean of our normal distribution is the output of an affine-linear function, which in turn has its own parameters $w$ and $b$! This is much closer to the models we will see in this class. However, right now we will still consider the distribution parameters $\mu$ and $\sigma$ directly. If we went through the derivation again, we would eventually end up with the formula for the log-likelihood of the dataset:

Note that we have written $\mu_i$ to denote that the mean is different for each data point, since it is the result of our linear model applied to $x_i$. Now we just have to insert the logarithm of the normal distribution:

Earlier, we assumed that $\sigma$ is constant. That means we only need to optimize for the mean $\mu_i = wx_i + b$. Since adding constants doesn’t change the optimization results, we can remove them:

After removing the additive constants, $2\sigma^2$ is now a lone multiplicative constant, which we can also remove. So we are left with

Recall that this is the log-likelihood we want to maximize. If we were to use a setup where we have a loss to minimize, we could simply remove the minus and minimize

It’s the sum of squared errors! Thus, it turns out this loss function is not arbitrary. Optimizing the sum of squares corresponds to maximum likelihood for a model with Gaussian likelihood and a fixed, constant $\sigma$.

Did that really help us? We wanted to use the squared error anyway! However, we gained two things:

1. We understood the assumptions implied by using squared error.
2. We could now construct regression models with non-Gaussian errors and derive appropriate error functions.

The second point is particularly relevant in cases where we have a principled reason to assume specific random components, e.g. in certain physical processes. Still, we should make clear that this doesn’t mean the log-likelihood is the only valid target, or that you are doing something wrong by choosing a different loss function. Maximum likelihood is simply a guiding principle which you may or may not use, and which can have disadvantages, as well.

Solving the Linear Case

Just for completion, for linear regression the loss would become

We can now compute the gradients with respect to $w$ and $b$:

You could use these to find a solution using gradient descent, or once again try to find the critical points where the derivatives are 0. This is left as an exercise for the reader. :)

Adding a Prior

Recall that a non-uniform prior on the parameters ($w$ and $b$ in this case) simply ends up being added to the log-likelihood. For example, we may have preference (a “prior belief”) for small weights. This could be achieved through a Gaussian prior on $w$ centered around 0, and with fixed $\sigma_w$.

Once again removing constants and flipping the sign to turn it into a loss, we end up with just

This means a 0-centered Gaussian prior on $w$ actually corresponds to the famous “L2 penalty”. Note that we kept the scaling by $\sigma_w$. This is because the prior is usually added to another loss (like the squared error), and so their relative scaling to each other becomes relevant. The smaller you choose $\sigma_w$ here, the larger the penalty will become. This makes sense: A smaller $\sigma_w$ implies a stronger belief that weights should be closer to 0, so any deviation away from 0 becomes worse.

At this point you may remember that the squared error loss also originally had a scaling by $2\sigma^2$. Shouldn’t we include that as well? However, if both the log-likelihood and the log-prior were scaled by different factors, we could re-scale the entire loss such that one of them is scaled by 1. For example:

This is prior + likelihood. We can multiply by $2\sigma^2$ to get

Multiplying by the constant $2\sigma^2$ does not change the optimal parameters, and so we only need a scaling factor on the prior! It just becomes a little more difficult to interpret, as it contains the variances for both the prior and the data. This is a slightly more advanced topic; don’t be too concerned if this is still somewhat confusing.

Conclusion

In this article we have seen how to interpret linear regression as a probabilistic model. This is arguably less intuitive than our previous coin flip example, but opens the door to even more complex models. For example, we have not yet considered distributions over higher-dimensional spaces (i.e. vectors). This will be the subject of a future post.

For now, it should be good practice to try out these concepts yourself. For example, what happens if you remove the assumption of constant variance? Or maybe replace the Gaussian distribution on the error $\epsilon$ by something entirely different? Being able to handle such questions is a prerequisite to really be able to develop new modeling approaches, rather than simply applying what is already there. Next time, we will be looking at generative models, where rather than modeling the relation between to variables, we will see how to model more complex higher-dimensional distributions. See you there!

In this post, we will first look at what probabilistic modeling actually is, by considering the example of a coin flip. In the next one, we will then look at linear regression through the probabilistic perspective.

Flipping Coins

Consider what happens when you flip a coin. You throw it, it flips around a few times in the air, and lands either heads or tails up. Now, what if I asked you to predict which side is going to land up? Most likely, you will just make a guess, and you expect to have a 50% chance to be correct (assuming the coin is fair). You would probably say that the result is “random”. But what does that mean?

Probabilities as Abstraction

The coin flip process seems pretty simple to understand. When you throw it, a certain side is showing up. Let’s say heads. While in the air, it will flip a few times. If it doesn’t flip at all, it will land heads up. If it flips once, tails up; twice, heads up; thrice, tails up, etc. It seems all we need to know to “predict” the result is a) which side is up before the throw, and b) how many times the coin will flip while in the air.

Now, I’m no physicist, but it sounds like this should be possible. Given exact information about the force behind the throw, the “angular momentum” of the coin, maybe air resistance etc., we should be able to derive how many times the coin is going to flip, and thus perfectly predict the result. I would think that it’s possible to build a “coin flipping machine” that would always produce a coin flip with the desired outcome. There is really nothing “random” about this!

And yet, this is clearly not feasible for a human, looking at another human flipping a coin. There are too many factors interacting in too complex of a way. And so we make the abstraction of saying that the flip is essentially random, even though this is not really true – it’s just a lot more manageable as well as practically useful.

As such, we create a probabilistic model of the coin throw: We assume that there is some probability $\theta$ that it will land heads up, and accordingly it will land tails up with probability $1-\theta$¹. If we denote heads by the number 1 and tails by 0, this can be summarized via the following expression:

This is called the Bernoulli distribution for binary numbers. If the coin is fair, we expect $\theta = 0.5$. This extremely simple model fully describes our abstraction of the coin flip process.

Learning About the World With Models

Once we have a model of some real-world process, we can use it to learn about the world. Let’s say we are playing a coin flipping game, where I flip the coin, and you have to guess the outcome for the possibility of a reward. Now, assuming that I haven’t mastered the art of coin flipping to the degree mentioned earlier, this is simply a guessing game. However, what if the coin is not fair? That is, the coin might land heads up with a probability $\theta \neq 0.5$. Long term, this will skew the results and might throw off your guessing. Let’s say you get suspicious and start tracking the results. After $n$ throws, we got $k$ heads, and $n - k$ tails accordingly. Intuitively, you would probably say that if $k / n$ is too far from 0.5, you conclude that the coin is not fair. But can we formalize this somehow?

Maximum Likelihood

We could say that we want to find the best model given our observations. But what is “best”? One way to formalize this is using probability theory: We want to find $\arg\max_\theta p(\theta | X)$, where $\theta$ represents our model (in this case, just one probability) and $X$ our data (a collection of many coin flips). What exactly we mean by “probability of a model” is a bit of a philosophical topic and beyond our scope here, but we can take it to mean “how much do we believe this model is true”, or just some kind of “score” for the model. That is, we want to find the model with the highest score or believability. Now, Bayes’ rule tells us that

We seemingly made the expression more complex – we replaced one probability by three! However, because we only care about which $\theta$ is the best, and not the actual value, we can disregard $p(X)$, as this is just a constant multiplier:

Here is a graph showing a function shifted or scaled by a constant – note how the maximum remains at $\theta = 0.5$:

In the equation above, $p(X | \theta)$ is called the likelihood, and $p(\theta)$ the prior. The prior basically gives our beliefs about the model before we have seen any data. For example, we may assume that the coin is probably fair, because most coins are. Then, the prior would be larger for values of $\theta$ around 0.5. For simplicity, we will assume a uniform prior, i.e. $p(\theta) = c$ for some constant $c$. Then, the prior is also just a constant multiplier, and we are left with the likelihood $p(X | \theta)$ as the target to maximize:

Since this is called the likelihood, and we want to maximize it, this procedure takes the name maximum likelihood.

Deriving a Solution

Let’s find the optimal $\theta$. To start with, our data $X$ consists of many coin flips $x_1, x_2, \ldots, x_n$. These coin flips are independent, that is, the result of one flip does not influence the next. They are also identically distributed, i.e. $\theta$ is the same for all flips. Since probabilities of independent events factorize, we get

This is great, because it allows us to think just about probabilities of single coin flips. As we have described further above, these follow a known distribution, the Bernoulli distribution. Unfortunately, the above expression is not quite usable in practice, since it involves a product over potentially many numbers, quickly leading to numerical issues. Thus, we usually work with the log-likelihood instead:

The fact that the logarithm of a product is the sum of logarithms allows us to avoid multiplying $n$ numbers. And as it turns out, log probabilities often have a simpler functional form, as well. Now we are at a point where we can insert the Bernoulli distribution:

Our goal is to find the parameter $\theta$ which maximizes this expression. Recall from calculus that a necessary condition for a maximum is that the derivative is 0 at that point. Thus, we can compute the derivative, set it to 0 and solve for $\theta$. The derivative is given by

Earlier, we assumed $k$ heads in our data and thus $n-k$ tails. $x_i$ is 1 for heads and 0 for tails, and $1-x_i$ is 1 for tails. Thus, the sum simply evaluates to

Setting this to 0 gives

Solving this for $\theta$ is slightly annoying, and there are different ways to do this. Here is one:

Thus, the optimal $\theta$ is just the proportion of heads we saw, which is most likely the intuitive solution you would have come up with anyway! Note that technically, we would still have to check whether this is really a maximum (e.g. using the second derivative). We would also have to treat $k=0$ or $k=n$ as special cases (since we would be dividing by 0 above). However, we will skip these details here.

That the point we found is indeed a maximum can be seen when plotting the log-likelihood. For the graph below, we created random data that is 1 with a certain probability $\theta$, and 0 otherwise. For each graph, we use different $\theta$ and do 10,000 flips. We only show $\theta \leq 0.5$ since probabilities larger than 0.5 would look symmetric. For example, the likelihood for $\theta=0.9$ is a mirrored version of $\theta=0.1$.

Advanced Considerations

Revisiting the Prior

Remember that earlier, we simply disregarded the prior on $\theta$. What if we want to include it? Turns out that’s pretty simple. For our target, we would be left with

That is, we simply have to add the log prior. We of course have to choose a distribution; this is a topic going way beyond our scope. However, given that this has to be a distribution over $\theta$, which is a probability, this should be a distribution over the range [0, 1]. A common prior for Bernoulli likelihoods is the Beta distribution. This has

where $B(\alpha,\beta)$ is the so-called Beta function and $\alpha, \beta$ are distribution parameters. In fact, they are hyperparameters that shape the prior on our parameter $\theta$. We will have to choose these appropriately.

This seems complicated. But: When taking the derivative with respect to $\theta$, the Beta function disappears completely, since it is independent of $\theta$. What we are left with then looks a lot like our previous log-likelihood! It turns out a Beta distribution with given $\alpha, \beta$ is equivalent to seeing $\alpha-1$ many heads and $\beta-1$ many tails. For example, if we set $\alpha = \beta = 501$, that is the same as having seen 500 heads and tails before ever having seen any actual data. This reflects a relatively strong prior belief that the coin is fair, and we would need to see a lot more data to convince us otherwise. For example, say you did 1000 flips and saw 800 heads and 200 tails. The maximum likelihood solution would then be $\theta = 800/1000 = 0.8$. But with the aforementioned prior, it would be $1300/2000 = 0.65$.

Connecting to Machine Learning Concepts

Let’s look again at our log-likelihood: $ x_i\log(\theta) + (1-x_i) \log(1-\theta)$. If you put a minus in front of this, what do you get? It’s actually the binary cross-entropy, the loss function you would likely choose when training a neural network on a binary classification problem (e.g. using a single sigmoid output). It turns out the concepts discussed here work in the same way if you replace the fixed $\theta$ by the output of a neural network. Thus, the choice of binary cross-entropy as a loss function is not arbitrary; it corresponds to the maximum likelihood solution!

One fine difference you may have noted is that we are usually averaging over examples for our loss functions, whereas here we are summing. But that isn’t really an issue, since the average is just the sum divided by the number of examples – a constant multiplier! Thus, the solution doesn’t change whether we are summing or averaging.

We can also understand the prior from a different perspective: $ \log(p(\theta)) + \sum_i \log(p(x_i | \theta))$. On the right, we have the “loss function” for our data. On the left we are adding a term independent of the data, only dependent on the model. This is a regularizer! See it the other way: By adding, for example, a weight penalty on a loss function, you are encouraging smaller weights. You are basically expressing a prior belief that the “correct” model has small weights, with the size of the regularization parameter determining the strength of your belief.

Conclusion

This was a first look at understanding data and models through a probabilistic lens. To summarize:

• Real-life processes may be modeled as abstract probabilistic processes.
• Given some data, we can look for the model that best fits our observations.
• A principled way to find a good model is using maximum likelihood, optionally including a prior.

We will expand upon these concepts in the class. For many generative models, it is possible to implement and work with them without having a solid grasp of what is actually going on in the background. But for a Master’s level class, we should aim for a higher level of understanding, and these concepts form the basis. Review them as necessary and clarify doubts in class! In the next post, we will understand linear regression as a probabilistic model, as well. See you there!

VQ-VAE Basics

VQ-VAEs were introduced in 2017 for discrete representation learning. In a standard autoencoder, data points are mapped to arbitrary latent representations. In variational autoencoders, each data point is mapped to a probability distribution instead. Usually, continuous distributions are chosen, with the most common choice being Gaussians. VQ-VAEs, on the other hand, encode data to discrete representations. To achieve this, first a regular autoencoder is applied. Next, each latent vector is mapped to the closest vector in a codebook, which is also part of the model, and learned alongside the other parameters. This means that the latent representations are limited to combinations of the codebook vectors. For more details, please read the paper linked above.
The discrete latent space has some unique advantages over regular VAEs. For example, we can compress high-dimensional data to a smaller discrete representation, and then train an autoregressive model to generate such representations, which can then be decoded back into the original space. Such techniques are used in models like MusicGen to generate music with high sampling rates relatively efficiently.

Compression With Autoencoders

VQ-VAEs have a major advantage over regular autoencoders in terms of the compression they can achieve in the latent space. As an example, let’s say we are working with color images of size 256x256. Perhaps we train a convolutional autoencoder to compress these to a size of 32x32. On the surface, this seems like a reduction by a factor of 64, since that’s the reduction in the number of pixels. However, we generally have a larger number of channels in our latent representation! Color image have three channels, but our encoding may have a lot more. Let’s say we have 256 channels in the latent space. This is more than 80 times more than the input, completely negating the reduction in pixels! Additionally, we usually encode to floats, which are often stored at 32bit precision, whereas images are often only stored in 8bit precision. This means our autoencoder blows up the representation by another factor of 4! Overall, our “compressed” latent representation takes more space than the original images. Of course, we could play around with the parameters to alleviate this, but we will have a hard time achieving strong compression while retaining good reconstruction quality.

This is where VQ-VAEs shine: Since we have a limited number of codebook vectors, and we know that each “pixel” in the encoding is one of those vectors, we do not actually need to store the full encodings. Rather, we only need to store, for each pixel, the index of the codebook vector at this point. The codebook, meanwhile, needs to be stored only a single time, no matter how many images we encode. The number of bits per codebook index depends on the size of the codebook. For example, a codebook with 1024 entries would require indices from 0 to 1023, which require 10 bits to store. Thus, in this example, each pixel would only require 10 bits to store the index, down from 32*256 in the example above (32 bits per float times 256 channels). Finally, we can actually achieve proper compression!

Exploring Compression

When training autoencoders, there are many moving parts: Dataset, architecture, latent space structure, reconstruction loss… I conducted some experiments where I tried to simplify things as much as possible. I trained a convolutional autoencoder to minimize mean squared reconstruction error on CIFAR10. The architecture is fixed, except for the number of channels d in the final encoder layer, which are varied systematically. As such, images are encoded to 4x4xd, down from the 32x32x3 input size. The results can be seen below.

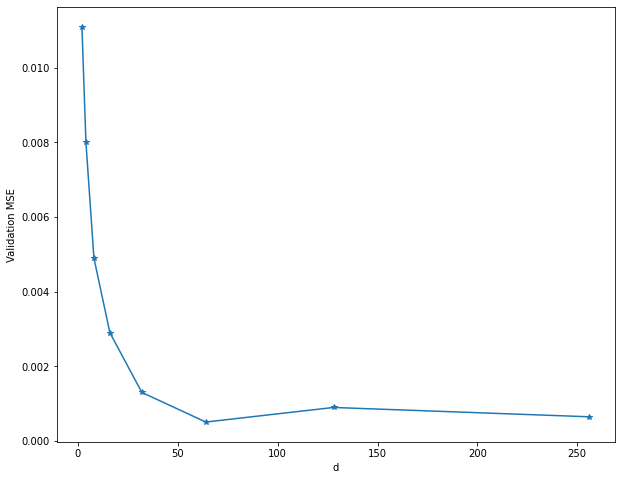
Unsurprisingly, more channels, i.e. a larger latent space, results in better reconstructions, as the model can simply store more information in a larger space. I’m not sure why performance slightly degraded when using d=128; there may have been some instability in the training as the model starts to overfit. Subjectively, a loss of around 0.002-0.003 is where the reconstructions start looking “acceptable”, so in this case, d=16 is a kind of lower bound for acceptable performance. Of course, a different (e.g. larger) architecture may be able to compress more efficiently, and thus manage with a smaller d. On the other hand, performance plateaus after d=64. My goal here was not to find the best possible architecture; rather, this just serves to provide a baseline performance for the following VQ-VAEs.

Introducing VQ

When using VQ-VAEs, we introduce another main variable: Codebook size k. That is, in addition to d, how many vectors do we allow in the codebook? Obviously, more vectors can cover the latent space more densely, which should be beneficial for reconstruction performance, as the quantization becomes more precise. Compare the two figures below; each orange cross is one codebook vector. The first only uses 8 codebook vectors, the second one uses 512.

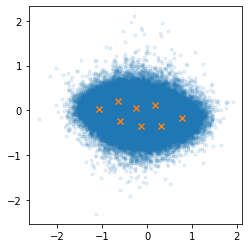
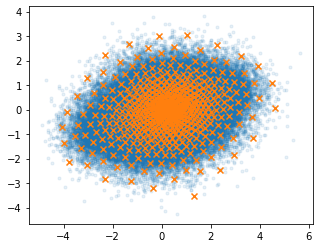
However, more vectors also means less compression. As such, we only want to use as many vectors as actually necessary. Here are the results; this time, each d is represented by a different line, whereas the new parameter k is on the x-axis.

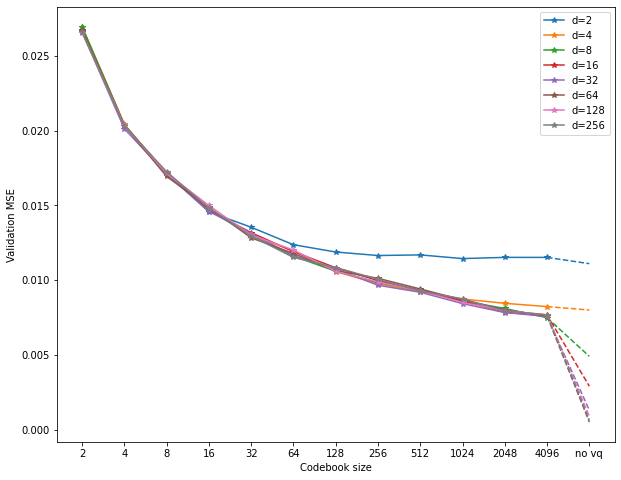
Things look quite a bit different this time: While performance still improves with larger d as well as k, there is an interaction between the two. To be precise, codebook size k seems to put a hard limit on the benefits of larger d. In fact, even with a rather large 4096 codebook entries, performance maxes out at d=8, with no benefits for more latent channels. Also, already for d=8, performance lags far behind the basic no-VQ autoencoder. It seems an absurd number of codebook entries would be required to catch up.

These observations make sense: For larger d, the overall size of the space increases exponentially. As such, we require many more codebook entries to properly “fill out” the space. Thus, we quickly arrive at a situation where the model cannot make use of the larger d, as the codebook vectors simply cannot make use of the available space.

This obviously presents us with a bit of a problem. If VQ-VAEs result in unacceptable reconstruction performance, their compression advantage is not useful. Recall that I mentioned a loss of around 0.002-0.003 is a good minimal target for this task. None of the VQ models even come close to this value, in fact barely reaching around 0.007 or so. Increasing the codebook size becomes infeasible at some point.

We can understand this mathematically. Recall that, for k=1024, each “pixel” in the encoded image requires 10 bits to store the codebook index. This is the “bit depth” of each sample. Also, in our architecture, we encode each image to a 4x4 array of indices. That is, there are 16 vectors per image. This puts us at 16*10=160 bits per image. Compare this to the original: 32x32 pixels, 3 color channels, 8 bits per value. This puts us at 32*32*3*8 = 24576 bits per image. We are compressing by a factor of 153.6. What if we are okay with more bits, i.e. less compression? We can either increase the number of vectors, that is, compressed image size (say, to 8x8), or the bit depth. Increasing the image size can have negative consequences for downstream applications. For example, if we wanted to train a generative model on the latent space, we only need to generate 16 vectors for a 4x4 image, whereas we would need 64 vectors for an 8x8 image, meaning four times more effort. The other option is to increase bit depth, which is drectly related to codebook size k. Maybe we are okay with 2x less compression, i.e. increasing bit depth from 10 to 20. But 20 bits correspond to 2**20 codebook entries – over a million! This is infeasible, and hints to why increasing k is not effective: Each doubling of codebook size adds only a single bit of information per vector. Clearly, we need some other method to increase the capacity of our codebooks.

Residual VQ

The basic idea of residual VQ (RVQ) is to use a series of codebooks applied in sequence. After applying one codebook, there is generally some degree of quantization error, i.e. the difference between the quantized vector and the pre-quantized encoding. RVQ then applies a second codebook to quantize the quantization error, which is just another vector. This will incur yet another quantization error, which can be quantized via a third codebook, and so on. The final quantization is the sum of all per-codebook quantizations.

This is an efficient way to achieve higher bit-depth: If one codebook with 1024 entries takes 10 bits, then two such codebooks use 20 bits, with only 2048 vectors overall. Recall that a single codebook would require over a million vectors for 20 bits. There is also an intuitive way to understand this: One codebook with 1024 entries obviously only gives 1024 options for quantized vectors. But with two codebooks, each entry in the first can be paired with each entry in the second, giving 1024*1024 entries, i.e. 2**20 or over a million, the same number of options as a single codebook with a million entries. The effect becomes more dramatic with more codebooks, exponentially increasing the number of possible quantizations. All in all, this provides an efficient way to significantly increase bit depth for our VQ-VAEs. Here are some results for our CIFAR10 task:

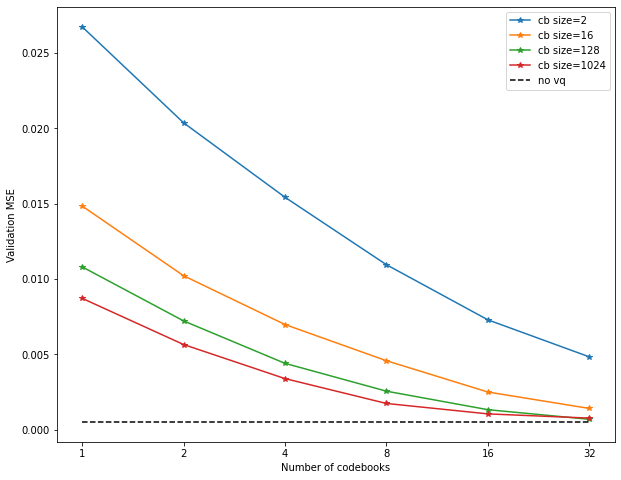
Here, d=64 was fixed, as this was sufficient for optimal performance in the no-VQ condition. Codebook size and number of codebooks was varied. As we can see, even with only two vectors per codebook, by using enough codebooks, we can achieve decent performance – actually better than with a single codebook with k=4096 in the previous experiment, even though using 32 codebooks we only have 64 vectors overall. Using larger codebooks, we can finally approach no-VQ performance.

There are different ways to interpret these results. Having “number of codebooks” on the x-axis is not really fair, since the models using larger codebooks of course have many more vectors overall. We can re-order the curves to have “total number of codebook vectors” on the x-axis:

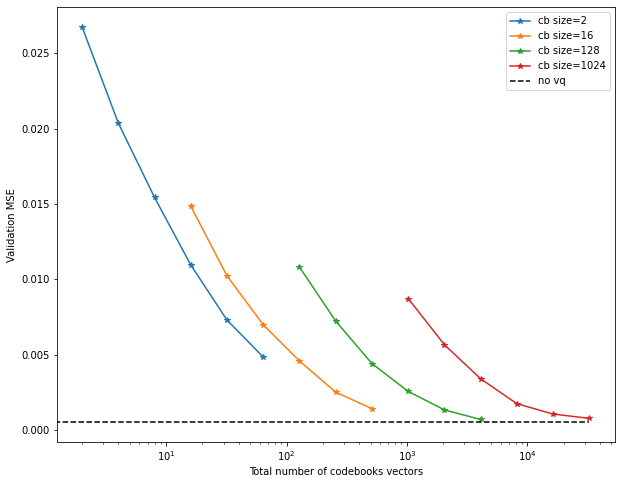
This is simply k * number_of_codebooks. This now seems to imply that using many smaller codebooks is actually more efficient in terms of performance. So is the answer to just use a huge number of size-2 codebooks? Not really. Recall that, at the end of the day, our main concern may be the degree of compression of the data, i.e. bit depth. 32 codebooks of size 2 may have 64 vectors overall, but the number of bits here is also 32 – one bit per codebook. On the other hand, a single codebook of size 64 only requires 6 bits. Thus, it may be a better idea to sort the x-axis by number of bits required:

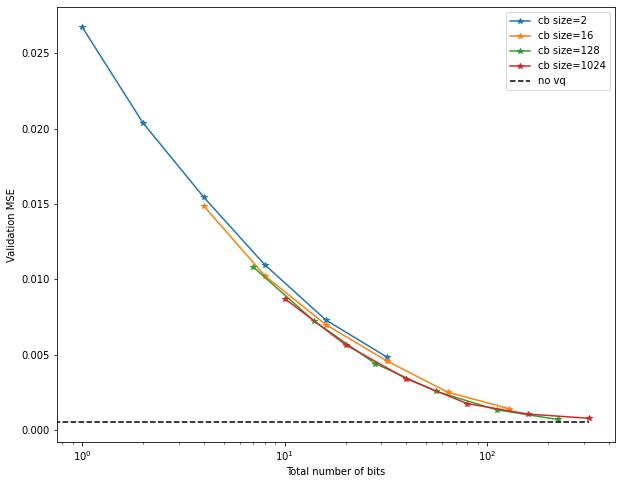
This reveals yet a different picture – it seems to barely matter what combination of codebook size and number we use to achieve a given number of bits! If anything, this implies that larger codebooks perform slightly better. Another striking feature is the very clean functional form – looks like a power law could be a good fit, for example. Using this, it may be possible to predict in advance how many bits would be required to achieve a certain performance.
Finally, we can also use “possible number of quantizations” for the x-axis. For example, as mentioned earlier, two codebooks of size 1024 allow for around one million different quantizations.

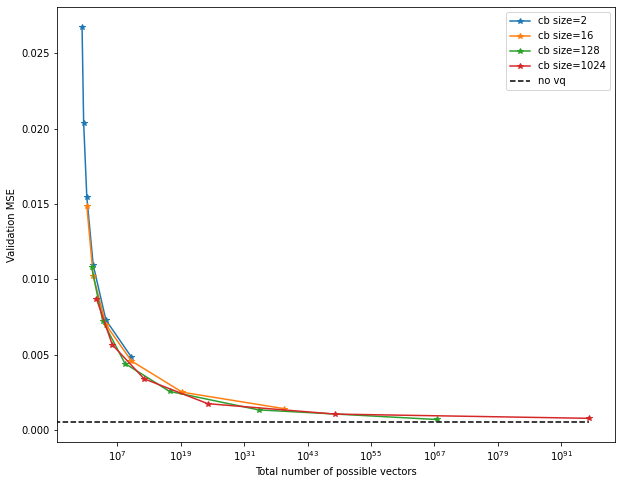
This looks similar to the previous plot, and that is no surprise – it turns out, the number of bits is just the (base-2) logarithm of the number of quantizations! As such, this is really just a re-scaling of the x-axis.

What About The Image Size?

To finish up, here is one more experiment: Recall that there are two ways to increase the overall number of bits: Increasing bit depth, or increasing the size of the encoded image. I wanted to see how the two relate, so I trained another set of models. These have basically the same architecture, but I cut off one set of layers to stop already at a resolution of 8x8. Results are shown below:

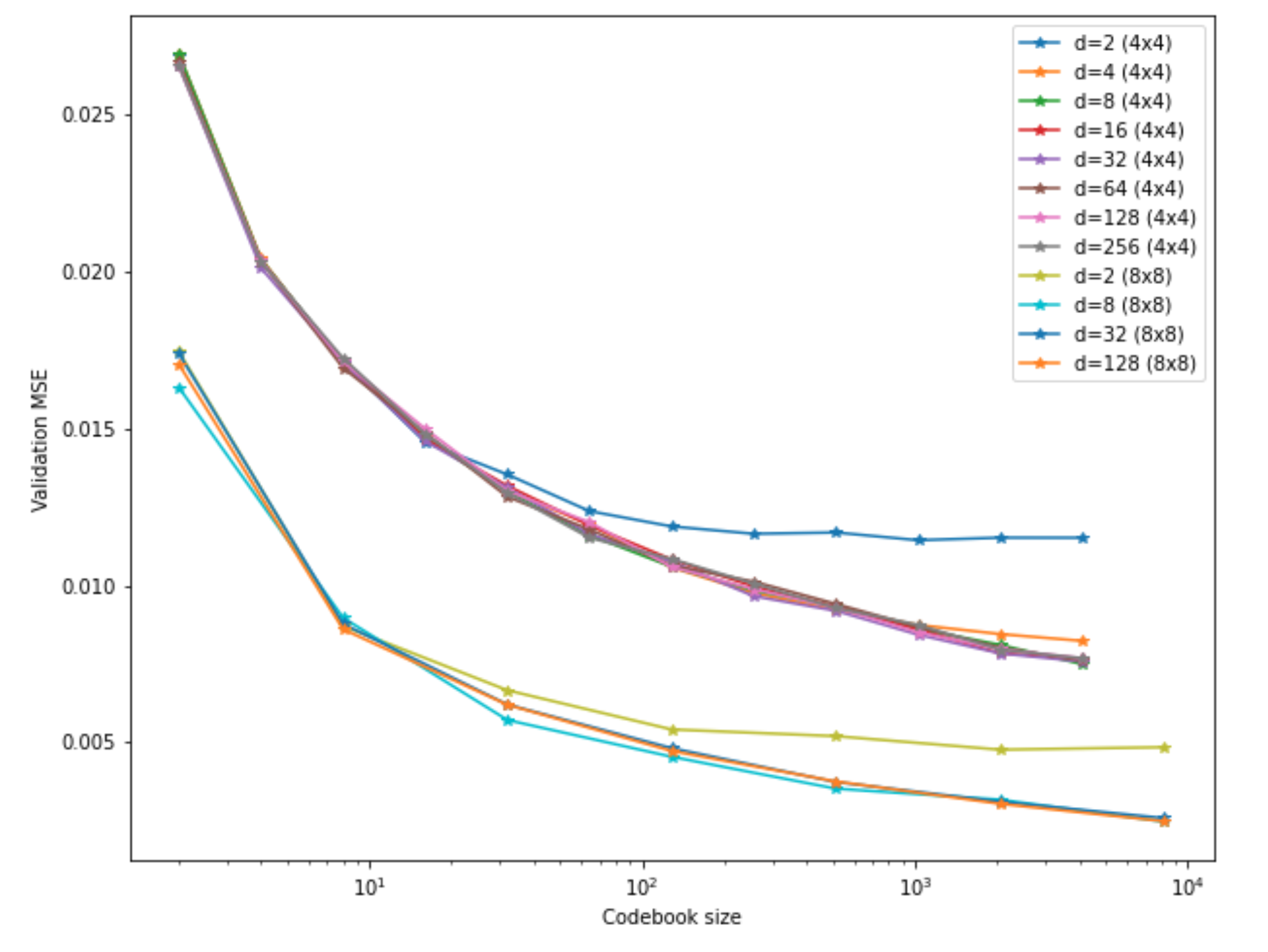
Here, I only tested the regular VQ-VAE, i.e. a single codebook, but varying number of entries k. This implies that, with the same codebook size, the 8x8 models perform better. But, of course, this is once again not a fair comparison: At the same bit depth (related directly to k), the 8x8 models have four times as many vectors in their latent space, and thus use four times more bits. We can once again equalize the x-axis by number of bits, this time for the whole encoded image:

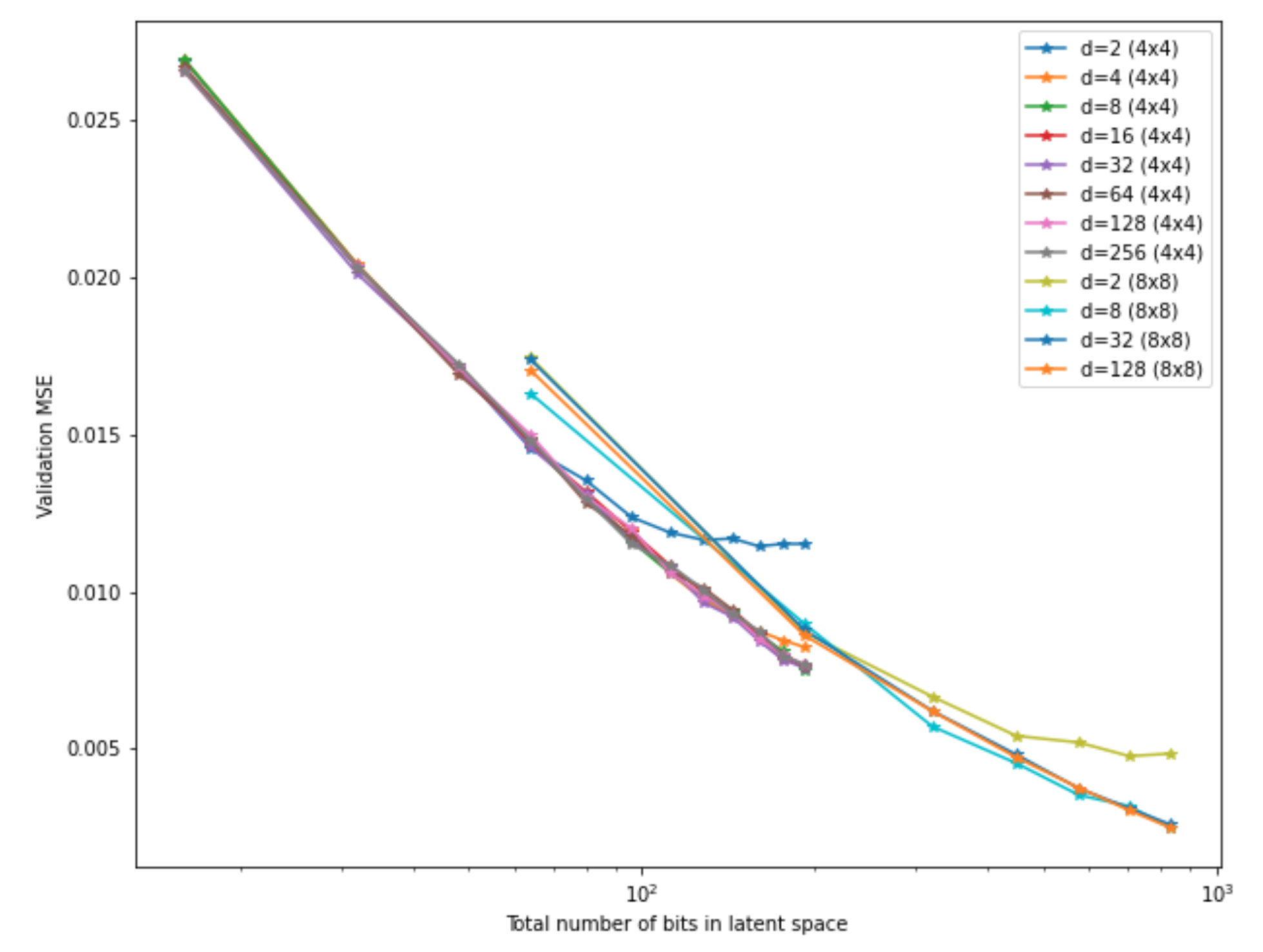
Looks like the 8x8 models actually perform worse! This once again shows how important it is to use the correct information on the axes. Of course, this could just be a quirk of the architecture design, since the 8x8 models simply have fewer layers, which could lead to weaker performance. This is not supposed to be an exhaustive test – I just wanted to showcase all the different factors we can vary.

Conclusion

We have seen that the number of bits in the latent space is key for good performance with VQ-VAEs. With a single codebook, it can be difficult to achieve higher bit rates, as these might require too many codebook vectors to be feasible. Residual vector quantization provides an interesting workaround; they seem to be a good option to achieve close-to-non-VQ performance. It remains to be seen whether such results generalize to more complex datasets and architectures. Here, other factors may start playing a confounding role, or more complex loss functions than MSE may not show the same predictable behavior. Still, it can be reassuring to see such clear and consistent behavior in the context of deep learning, where we often feel like we arestumbling through the dark when looking for improvements to our models.

One widely applicable technique to improve neural network optimization is batch normalization. When it was initially proposed, BN seemed like a simple way to massively speed up training and improve performance, with very few downsides. Over the years, however, cracks have begun to show: Why BN even works at all is debated (also see here or here or here…) and research has shown problematic behavior (e.g. here).

BN and GANs are combined in some architectures, such as the popular reference DCGAN. Although outdated, this still serves as an important go-to architecture when starting to learn about GANs, with sample code being available on both the Tensorflow and Pytorch websites. Notably, the DCGAN paper mentions that they use BN, but not in the final generator layer nor in the first discriminator layer, as this would cause unstable behavior. However, no explanations for this behavior are given, nor why removing BN from those layers specifically should fix it.

After running into strange issues and seemingly impossible behavior in my own research involving GANs, I decided to further investigate how these networks interact with BN. My findings up to this point are summarized in this blog.

Setting The Stage

Let’s train a small GAN on a simple toy dataset. See the dataset below; the goal is to learn a generator G that essentially transforms noise (drawn from a 2D standard normal distribution in this case, although this could be any distribution at all) into data samples. We will use Tensorflow/Keras, although none of the issues discussed in this post are framework-specific.

First, we set up simple networks for G and D:

generator = tf.keras.Sequential(
    [tfkl.Dense(64),
     tfkl.LeakyReLU(alpha=0.01),
     tfkl.Dense(64),
     tfkl.LeakyReLU(alpha=0.01),
     tfkl.Dense(2)], name="generator")

discriminator = tf.keras.Sequential(
    [tfkl.Dense(64),
     tfkl.LeakyReLU(alpha=0.01),
     tfkl.Dense(64),
     tfkl.LeakyReLU(alpha=0.01),
     tfkl.Dense(1)], name="discriminator")

We can train the GAN like this:

def train_step(real_batch):
    n_batch = tf.shape(real_batch)[0]
    noise = tf.random.normal([n_batch, 2])
    real_labels = tf.ones([n_batch, 1])
    fake_labels = tf.zeros([n_batch, 1])
    
    # train g
    with tf.GradientTape() as g_tape:
        fake_batch = generator(noise, training=True)
        d_out_deception = discriminator(fake_batch, training=True)
        deception_loss = -1 * loss_fn(fake_labels, d_out_deception)
    g_grads = g_tape.gradient(deception_loss, generator.trainable_variables)
    g_opt.apply_gradients(zip(g_grads, generator.trainable_variables))
    
    # train d
    with tf.GradientTape() as d_tape:
        d_out_fake = discriminator(fake_batch, training=True)
        d_out_real = discriminator(real_batch, training=True)
        d_loss = 0.5 * (loss_fn(real_labels, d_out_real) + loss_fn(fake_labels, d_out_fake))
    d_grads = d_tape.gradient(d_loss, discriminator.trainable_variables)
    d_opt.apply_gradients(zip(d_grads, discriminator.trainable_variables))
    
    return -deception_loss, d_loss

D is trained to classify real samples as 1 and fake samples as 0, guided by a standard classification loss (binary cross-entropy). G is trained to maximize this loss. We alternate one step of training G and one step of training D. The goal is for the networks to reach an equilibrium point where the distribution of samples generated by G matches the data distribution, and D outputs 0.5 for real and fake samples alike (that is, it “classifies” with maximum uncertainty). We run this training for 2000 steps using Adam. Note that we always put in the full population (2048 samples) as the batch in each training step. Here are the resulting samples:

As we can see, the generated samples match the data quite well. The loss for D in this case is around ln(2) ~= 0.69, which indicates outputs of 0.5 for all samples, as desired.

Introducing Batch Normalization

Now let’s add BN to our models. Of course, we don’t actually need to do this for this simple experiment, but let us assume we want to scale up our experiments to more complex data/networks, where BN could be helpful¹.

discriminator = tf.keras.Sequential(
    [tfkl.Dense(64),
     tfkl.BatchNormalization(),
     tfkl.LeakyReLU(alpha=0.01),
     tfkl.Dense(64),
     tfkl.BatchNormalization(),
     tfkl.LeakyReLU(alpha=0.01),
     tfkl.Dense(1)], name="discriminator")

We train the network in the exact same way as before and get this result:

It doesn’t look quite right, does it? Almost seems like the entire distribution is slightly shifted. Knowing that GANs have stability issues, we might just try again with a new initialization:

Now it’s definitely shifted in a different direction! And yet, in both cases, the observed loss is again around ln(2), indicating that D cannot tell the distributions apart at all.

Encouraging Distribution Shift

Let’s make the issue more obvious. We slightly change the loss used to train G like this:

deception_loss -= 0.005*tf.reduce_mean(fake_batch[:, 0])

This additional loss term encourages the generator to shift its generated samples positively on the x-axis (i.e. to the right).

The scaling is hand-tuned: It must be large enough to actually produce relevant gradients for the network, but if it is too large, G will essentially just ignore the adversarial game and infinitely decrease the loss by moving its samples further and further to the right. Empirically, with the scaling chosen as it is, G will not shift the samples if this causes it to lose out in the adversarial game (i.e. D easily tells the distributions apart since one is shifted). G will only shift samples if it can somehow do this without D noticing.

Using this loss, we get the results below:

This time, the shift is very obvious. Still, D still incurs a loss of ln(2), meaning it is completely fooled by the generated samples! Interestingly, if we remove BN but keep the additional loss term, we get this result:

No shift has occurred! It seems that without BN, D picks up on the shift and the resulting worse loss for G causes it to keep the samples where they should be.

Oh God, What Is Going On

It seems like our D is somehow blind to shifts in the data. The overall shape looks good, just not the location! The issue here is actually quite obvious when we take another look at the training code for D:

# train d
with tf.GradientTape() as d_tape:
    d_out_fake = discriminator(fake_batch, training=True)
    d_out_real = discriminator(real_batch, training=True)
    d_loss = 0.5 * (loss_fn(real_labels, d_out_real) + loss_fn(fake_labels, d_out_fake))
d_grads = d_tape.gradient(d_loss, discriminator.trainable_variables)
d_opt.apply_gradients(zip(d_grads, discriminator.trainable_variables))

Note that we put the real and fake samples into D separately. Recall that BN normalizes features using batch statistics. This means that the real samples will be normalized to mean 0 and variance of 1, and the fake samples will also be normalized to mean 0 and variance of 1².

This means that, if the fake samples are transformed by an affine-linear function (shifted and/or scaled by a constant), this will be normalized away by D, making it completely insensitive to such differences between distributions! In case this is not quite understandable yet, here is a simple example:

Say, you have two “real” and two “fake” samples with only a single feature. E.g. a_real = [0.5, 1.5] and a_fake = [6., 8.]. It would be very easy to tell these two apart. However, when each batch is normalized separately with their respective mean and standard deviation, they both result in [-1, 1]! Thus, any model working with the normalized data can never tell the two batches apart.

This is quite disastrous, as it means that G does not actually have to match the real data properly. Here, we have only seen affine-linear shifts being undetected. However, since BN is usually applied in all layers, it may be that higher-order differences between the distributions could also be normalized away in deeper layers (but so far, I have not been able to show this experimentally).

How Do We Fix This?

In the simple example above, what if we combine the two batches into one? Using a = [0.5, 1.5, 6., 8.] and normalizing this, we get [-1.12815215, -0.80582296, 0.64465837, 1.28931674]. As we can see, it is still easy to tell apart real and fake samples, e.g. with a threshold at 0.

This implies a straightforward solution: Use joint batches to train D instead³! This is what the training step for D would look like:

# train d
with tf.GradientTape() as d_tape:
    combined_batch = tf.concat([fake_batch, real_batch], axis=0)
    combined_labels = tf.concat([fake_labels, real_labels], axis=0)
    d_out_fake = discriminator(combined_batch, training=True)
    d_loss = loss_fn(combined_labels, d_out_fake)
d_grads = d_tape.gradient(d_loss, discriminator.trainable_variables)
d_opt.apply_gradients(zip(d_grads, discriminator.trainable_variables))

We train a model (with BN and without the additional loss term) with this and get the results below.

Oh no… This looks bad. Even stranger, the losses are 6.62 for G and 0.17 for D. Remember the equilibrium point 0.69? The loss for G is higher indicating that it’s “winning” the game against D. At the same time, the loss for D is lower, indicating that it’s also winning! How can this be possible?

A Step Back

Clearly, the above issue must be related to joint batches somehow, as that was the only change we made. Let us forget about those for a moment and just go back to split batches. Instead, I want to show the issue that originally made me launch this investigation. With the training step for D being as before (split batches), let’s look at the code for G instead, specifically the role of D:

# train g
with tf.GradientTape() as g_tape:
    fake_batch = generator(noise, training=True)
    d_out_deception = discriminator(fake_batch, training=True)
    deception_loss = -1 * loss_fn(fake_labels, d_out_deception)
g_grads = g_tape.gradient(deception_loss, generator.trainable_variables)
g_opt.apply_gradients(zip(g_grads, generator.trainable_variables))

We are calling D with training=True. But if you think about it, we aren’t really training D here, are we? What if we just set training=False? It seems more appropriate. Well, we get results like below:

This is even worse than above! Losses are 4.23 (G) and 0.007 (D), once again indicating that both networks seem to be winning the game at the same time. I want to stress that this is really not possible since we use the standard “zero-sum” formulation of the GAN game⁴. The only explanation is that somehow, G and D must be playing different games. Let’s finally try to fix this.

A Reminder About Batchnorm

Both failures shown above have to be related to Batchnorm:

1. Batchnorm is the only thing in D that introduces dependencies between batch elements, possibly causing different behavior between using joint or split batches.
2. Batchnorm is the only thing in D that has different behavior between training being True or False.

Specifically, during training, Batchnorm uses batch statistics to normalize features. During inference, however, this is undesirable as you don’t want predictions for one element to depend on those for other elements – you might not even have batches to run on, just single examples! For this reason, Batchnorm also keeps a moving average of batch statistics. As such, batch statistics are accumulated over the course of training, and when using training=False these accumulated statistics are used for normalization instead. This gives us a hint why approach 2 above didn’t work: There must be some difference between batch statistics and accumulated statistics.

The Issue With Approach 2

When using split batches for training D, both real and generated samples are normalized using their respective batch statistics. At the same time, these batch statistics are used to update the moving average population statistics. However, we only have one set of such statistics, while the real and generated statistics will likely be quite different (especially early in training). This results in the moving averages to be somewhere between the real and generated statistics, as exemplified below using the means:

When training G with training=False in D, these accumulated statistics are used to normalize the generated batch input in D. But since these statistics do not match the generated batch statistics, the inputs are not properly normalized! This issue gets worse in every layer that uses BN, and leads to D with training=False to essentially be a different function than with training=True. And this, finally, solves the riddle of how both networks can “win” at the same time: G is basically playing a different game! Clearly, we cannot train our GAN like this.

The Issue With Approach 1

Remember that using joint batches for D did not work, either. The issue is actually similar: When training D, features are normalized using the statistics of the joint batch. But when training G, we usually only feed a generated batch, which, of course, has different statistics. Again, this causes a mismatch between the D that is being trained, and the D that G trains on.

How Do We Actually Fix This?

Clearly, we have to resolve this mismatch somehow. Funnily enough, one possible fix is to actually combine the two approaches that did not work, i.e. D with training=False when training G, and joint batches for training D. The code then looks like this:

# train g
with tf.GradientTape() as g_tape:
    fake_batch = generator(noise, training=True)
    d_out_deception = discriminator(fake_batch, training=False)
    deception_loss = -1 * loss_fn(fake_labels, d_out_deception)
g_grads = g_tape.gradient(deception_loss, generator.trainable_variables)
g_opt.apply_gradients(zip(g_grads, generator.trainable_variables))

# train d
with tf.GradientTape() as d_tape:
    combined_batch = tf.concat([fake_batch, real_batch], axis=0)
    combined_labels = tf.concat([fake_labels, real_labels], axis=0)
    d_out_fake = discriminator(combined_batch, training=True)
    d_loss = loss_fn(combined_labels, d_out_fake)
d_grads = d_tape.gradient(d_loss, discriminator.trainable_variables)
d_opt.apply_gradients(zip(d_grads, discriminator.trainable_variables))

Now, when training D, the batches are normalized using the joint statistics. Also, the statistics of both real and fake samples are accumulated into the moving average. When training G, we only pass a generated batch to D, but because we set training=False, the accumulated statistics are used, not the ones of the batch. Finally, the mismatch is resolved! As we can see below, the model produces good samples, and it is even “immune” to affine-linear shifts in the data (like the original model without BN) due to the joint batch normalization.

It’s Not Over Yet…

Unfortunately, while the above works well for this simple toy example, I have still observed issues with both networks “winning” at the same time in larger-scale experiments. This implies that there must still be a mismatch in the normalization. Most likely, the accumulated population statistics (which are updated with a slow-moving average) lag behind the current batch statistics, especially early in training when the model parameters change rapidly. This could perhaps be fixed by making the average move faster, but this would make the population statistics more volatile and may reduce inference performance. To finish our investigation, I would like to discuss a few more possible solutions:

1. Also pass a joint batch to D when training G, and using training=True again. This guarantees consistent behavior in D for both training steps. The only annoyance is that this requires additional computation, as we have to put an entire real batch through D that we otherwise wouldn’t need, and that doesn’t influence the training of G directly (except through the changed statistics).
2. Don’t use BN. Overall, it seems like BN is falling out of favor somewhat. This likely has to do with the fact that models are getting bigger and bigger, being trained on many GPUs in parallel, and BN is not effective for small batches. Instead, other normalization methods can be used, such as Weight, Layer, Instance or Group Normalization. None of these methods introduce dependencies within a batch, and thus should produce less “strange” behaviors. However, another takeaway of this post should be that you have to think about what kind of information is “normalized away”. Remember that the original issue was that BN caused D to ignore affine-linear shifts (at the population level) in the data. If we look at Instance Normalization, this should be even worse, as it would normalize affine-linear shifts even at the instance level. However, since IN only makes sense for data with spatial dimensions (images etc), we cannot test it in the simple framework used for this post. This may be content for follow-up work. Layernorm, on the other hand, seems to be able to detect these shifts (why/how exactly, I still have to think about), and thus Groupnorm should, as well. Finally, Weightnorm doesn’t modify the features at all, so it should have no issues.
3. Don’t use BN in the first layer of D. This prevents the “normalizing away” of affine-linear shifts, and the first-layer features can pick up on them and “preserve” them throughout the network. The DCGAN paper, for example, simply states that they did this (also removing BN from the final layer of G) because the training would otherwise be unstable. However, they do not offer any explanations for why BN may be harmful. The question for me is whether BN in later layers could still be problematic, since it might normalize away “higher-order” differences in features that have the same mean and variance, but differ in higher moments.

A Bonus Experiment

Recall that our “broken” training attempts were caused by a mismatch between the distributions of the real and fake samples. Batchnorm normalizes the mean and variance. What if we force those to be the same between the distributions? Specifically, we transform our generated samples like this:

train_real_means, train_real_vars = tf.nn.moments(x_samples, axes=[0])
train_fake_means, train_fake_vars = tf.nn.moments(fake_batch, axes=[0])

fake_batch = (fake_batch - train_fake_means) / tf.math.sqrt(train_fake_vars)
fake_batch = fake_batch * tf.math.sqrt(train_real_vars) + train_real_means

Essentially, this works like a batchnorm layer with beta and gamma fixed to the statistics of the real data. Since we now force the statistics of the generated samples to equal the real data, there should be no more distribution differences, right?

Sort of. This actually works, if D has BN only in the first layer. It makes sense when you think about it: We equalized the means and variances of the real and fake data, so they will be “appropriately” normalized by the first-layer BN. However, the distributions are of course not identical; there will still be differences in higher moments. BN in later layers will still normalize these away, but because we did not equalize them between the distributions, we once again run into the old issues of G and D playing different games (samples being normalized with different statistics). To me, this indicates that BN in later layers can still be problematic, and just removing it from the first layer (as recommended in the DCGAN paper) may not be sufficient.

Takeaways

So is BN terrible and useless? Probably not. The issues discussed here only arise due to us training with two distinct populations (real and generated data). BN will likely still work well in many standard tasks in discriminative and generative modeling.

However, I think it’s important to be aware of the implications of normalizing this or that, completely removing certain information from your model in the process. In my personal experience, most normalization techniques are somewhat situational, and it is rarely clear in advance which one will work best for a certain task or model. Getting an idea of their respective quirks, however, can limit the search space and save lots of time.

And stay away from GANs, kids. ;)

I probably could have kept this post for myself, since the main reason I’m writing this is to force myself to better formalize and structure these ideas. But I also wouldn’t mind discussing these topics with other people. ;)

This will be a look at generative models for music from the perspective of a deep learning researcher. In particular, I will be taking the standpoint that such models should aim to possess some sort of creativity: Producing truly novel and “interesting” artifacts. To put it another way: They should model the process, not the data. I realize that many of the aspects I bring up are already being considered and actively researched in other communities (e.g. computational creativity). However, my main goal is to bring up specifically why some of the current research directions in deep generative modeling are (IMHO) misguided and why resources might be better spent on other problems.¹

Copying Is Not Creativity

Generative modeling may be summarized as: Given a set (or more generally, a domain) of data x, build a model of the probability distribution p(x). In fact, most “modern” deep generative modeling frameworks (such as GANs or VAEs)² do not actually represent this distribution, focusing instead on producing samples from p(x). The implications of this (e.g. preventing many potential applications of a generative model, such as inpainting or density estimation), while certainly important, are not the topic of this discussion. Instead, I want to focus on the case where generating outputs is all we care about.

While such models are mostly built and tested in the image domain (especially faces), attempts at creating music “from nothing” are becoming more ambitious (e.g. Music Transformer, Musenet, or most recently Jukebox). These models are certainly great accomplishments of engineering, since musical data (especially on the raw audio level) is very high-dimensional with dependencies across multiple (and very long) time spans. But what is their value, really? No matter how many layers the model has, how many units per layer, or which fancy connection schemes and training tricks are used – at the end of the day, the model will capture statistical relations between data points, because that’s what we ask it to do. Better models and/or smart conditioning on factors such as musical style, composers, lyrics etc. may mask this somewhat, but it doesn’t change the fundamental nature of these models – produce things that are like the things they have seen (or rather, been shown) before. ³ The inadequacy of this approach will be discussed further in the following sections, where I will sometimes refer to such models as copy models (please take this as somewhat tongue-in-cheek).

Please note: I am aware that there are contexts/applications where training a generative model to “copy” a distribution is actually the goal, and there is nothing wrong with that. However, models like the ones mentioned above are usually presented “as is”, with their ability to generate an endless stream of music as the main selling point. Interestingly, they are often explicitly advertised as generating music “in a certain style”, which IMHO masks their limitations somewhat by pretending that generating hours of Mozart-like music (for example) is the whole point. Of course, there is some value here – namely, exploring/showcasing model architectures that are capable of the kind of long-term structure needed to produce music. I’m certainly not proposing to get rid of deep models altogether – their incredible expressiveness should be leveraged. But I believe that at some point, the relentless scaling-up should be stopped, or at least halted for a bit, and the insights be applied to more creative approaches to making music.

As an approach radically different from copy models, it might be possible to start generating artifacts (e.g. pieces of music) without any reference data whatsoever. This will likely result in pieces that seem very alien to us, since they are not at all grounded in our own experience. Still, I believe it could be interesting to see where, for example, purely information-theoretical approaches could take us. That is, art should be predictable (so it is “understandable”), but not too predictable, since that would be boring/not stimulating. The process could additionally be equipped with simple sensory priors (e.g. related to harmony) to make the results more familiar. Such models could be used to investigate many interesting questions, for example: Under which models/assumptions is human-like music possible to evolve? When adding more assumptions, does it eventually become inevitable? Speaking of evolution…

There Is No Goal

Given a fixed data distribution for training, a generative model will be “done” eventually. That is, it will have converged to the “best” achievable state given the architecture, data, learning goals, training procedure etc. If we then start sampling thousands upon thousands of outputs (compositions) from the model, these will all come from the exact same (albeit possibly extremely complex) distribution. Diversity can be achieved by using conditional distributions instead, but these will still be stationary.

It should be clear that this is not a reasonable model of any creative process, nor will it ever create something truly novel. On the contrary, such a process should be non-stationary, that is, always evolving. New genres develop, old ones fall out of favor. Ideas are iterated upon. New technology becomes available, fundamentally disrupting the “generative distribution”. Such things should (in my opinion) be much more interesting to model and explore than a literal jukebox.

Concretely, I believe that concepts from research on open-endednessshould be very interesting to explore here. One example might be co-evolving generators along with “musical tastes” that can change over time. Speciation could lead to different genres existing in parallel. A minimal criterion approach could guarantee that only music that actually has listeners can thrive, while at the same time making sure that listeners like something instead of just rejecting everything for an easy “win”. Importantly, this allows for modeling the apparent subjectivity/taste that plays a big role in human appreciation of art, without relying on black-box conditioning procedures using opaque latent codes or similar approaches.

To expand upon the speculation on “ex nihilo” generative models at the end of the last section, it could be interesting to train a copy model to initialize an open-ended search process which is then perhaps guided by more general principles/priors. This would allow for exploring possible evolutions of existent musical genres.

The Right Level of Modeling

Generative modeling of music is usually done at one of two levels.

Symbolic

The first one is the symbolic level, where music is represented by MIDI, ABC notation, piano rolls or some other format. What is common to such representations is that they use (often discrete) “entities” encoding notes or note-like events in terms of important properties such as the pitch and length of a tone. Importantly, there is no direct relation to audio in these symbols – the sequences need to be interpreted first, e.g. by playing them on some instrument. This implies that the same MIDI sequence can sound vastly different when it is interpreted via two different instruments. This is arguably already a problem in itself, since widely used symbolic representations lack means of encoding many factors that are important in contemporary music (electronic music in particular).
In that regard, it is quite telling that many symbolic models are trained on classical (piano) music. Here, the instrument is known and fixed, and so it can be assumed that a “sensible” sequence of symbols will sound good.⁴

However, there is a second problem related to the interpretation of musical symbols, which is perhaps easier to miss. Namely, the symbols have absolutely no meaning by themselves. Previously I said that they usually encode factors such as the pitch or length of a tone – but the exact relationships are imposed by human interpretation. Take the typical western twelve-tone equal temperament (which MIDI note pitches are also commonly mapped to) as an example: Here, every twelve tones are one octave apart (i.e. they double in fundamental frequency). Seven tones (a fifth) are in a relation of 3:2, etc. Generally, every tone increases in frequency by about 6% compared to the next-lower one. Such intervals undoubtedly play an important role in human perception of music. But these relations are completely absent from a symbolic note representation. For a model training on such data, there might as well be five tones to an octave, or thirteen, or… The concept of intervals does not arise from symbolic data, and thus a model trained on such data cannot learn about it.

Then why do such models manage to produce data that sounds “good”, with harmonic intervals we find pleasing? This is simply because the models copy the data they receive during training. If the data tends to use certain intervals and avoid others, the model will do so, as well. The difference is that the training data was generated (i.e. the songs where composed) with a certain symbol-to-sound relationship in mind (e.g. twelve-tone equal temperament). However, this relationship is lost on the model, which merely copies what is has been taught without understanding the ultimate “meaning” (in terms of actual sound). In fact, this seems incredibly close to John Searle’s famous Chinese Room argument. Thus, unless one wants to view music generation as an exercise in pure symbol manipulation, the symbolic level seems unfit for any kind of music generation that is not content with merely copying existing data, although possible remedies could be to use more expressive symbols that relate more closely to the audio level (e.g. using frequencies instead of note numbers), or equip the model with strong priors informed by this relationship.

Waveform

Aside from the symbolic level, it is also possible to directly generate data on the audio (waveform) level.⁵ However, this approach has so far been lagging behind symbolic models in terms of structure, coherence and audio quality. Some models were developed on the single-note level (e.g. GANSynth), with a focus on quality. While such models are interesting for creative applications in human-in-the-loop scenarios (e.g. sound design), they are obviously not capable of producing interesting musical sequences. Still, there have been examples of modeling sequences in the waveform domain with some success (e.g.DAA).

Recently, OpenAI released their Jukebox model, which scaled up waveform generative models to levels far beyond what has been seen before. The fact that a single model can produce samples of such variety, conditioned on styles and even on lyrics, is astounding. However, there are still some issues with generating at the audio level:

1. Fundamentally, the model still tries to copy the training data.
2. The symbolic level is completely removed. Personally, I don’t think this is the right approach, either. It means that the model has to essentially discover concepts such as note events, tempo, rhythm etc. on its own. In a sense, it is lacking knowledge of how to make sounds, i.e. what instruments are there and how can they be played. Note that this is likely alleviated by using models such as VQ-VAEs which at least enforce some kind of discrete representation in the hidden space, but these are not necessarily connected to useful/interpretable musical concepts (certainly not when the model is initialized).
3. As it stands, most waveform generative approaches lack priors regarding the kind of data they produce, i.e. oscillating waveforms. This means that not only does the model have to learn what useful “sound sources” would be (see above), it also needs to learn how sound itself “works”, that is, to create oscillations at certain frequencies. This causes waveform models to produce audible artifacts as they struggle to adhere to clean oscillations. A possible remedy for this are approaches like DDSP.

Hybrids

It may be possible to combine symbolic and waveform approaches to achieve the best of both worlds. Essentially, this means using a symbolic-level model to produce sequences of symbols, and then a waveform model that translates those symbols into sound. This preserves many advantages of symbolic models (e.g. explicit, interpretable representations and specific ways of making sound) while also allowing the model to “connect” with the domain we eventually care about (audio).

While this sounds good in theory, there are of course problems with this approach, too. The main one is probably how to formulate a joint model for symbols and sound. A major obstacle here is that it is not possible to backpropagate through discrete symbols. Since most symbolic models output soft probability distributions over symbols, this is not a problem in the pure setting. But a joint model would probably not be able to work with such soft outputs, since it would be like “pressing every piano key a little bit, but one more than the others”. Still, there are workarounds for this issue, such as vector quantization with straight through estimators – or dropping gradient-based methods entirely and using alternatives like reinforcement learning or evolutionary computing instead.

Besides this problem at the symbolic level, there is also one in the symbol-to-audio pipeline: This generator needs to be differentiable, too. This means we cannot simply train a symbolic model with a “real” piano (samples), since the instrument cannot be backpropagated through. Alternatively, using standard neural network architectures (e.g. Wavenet) can lead to artifacts and/or slow generation as discussed before. Personally, I am really interested in approaches like DDSP that preserve differentiability while incorporating a sensible inductive bias for audio, leading to much better quality with simpler models.

A possible hybrid approach could go like this:

1. Train a DDSP model on instrument samples, say, a piano.
2. Train a symbolic model, but not on a symbolic loss; instead, use the trained DDSP network to turn the symbols into audio and compute a loss (or some other target function) on the audio level. Gradients can be backpropagated through the DDSP model, which should not (need to) be trained anymore, and then through the symbolic model – assuming the problem of non-differentiable discrete symbols (i.e. the transition between the two levels) can be solved somehow.

Perception

Colton argues that a creative system needs to have three distinct properties:

1. Imagination, or the ability to create novel artifacts. Models that learn and sample from p(x) arguably have this to an extent, in that they can draw samples that have never been seen before. On the other hand, as argued above, these models cannot move beyond p(x) and are thus unlikely to produce something truly novel.
2. Skill, or the ability to create quality artifacts. I would argue that this is the only property that standard data-driven generative models fulfill – given that they have enough capacity and are well-trained, outputs can be quite impressive.
3. Appreciation, or the ability to judge the novelty an quality of their own creations.

Heath & Ventura argue that this third point is a key component that is lacking in many generative systems. We can find analogues, however, in some modeling frameworks: (Variational) Autoencoders have an inference network (encoder) that can process data, which would include its own outputs. However, it is not clear how one would connect this to “appreciation”, since the main point of the encoder usually is to simply map the data to a lower-dimensional representation. Still, perhaps it could be easier to work in this space than in the data space directly.

On the other hand, autoregressive models as well as flow-based models (which generalize the former) can explicitly compute probabilities for a given data point, which might be taken as a proxy for “quality”. A model could use this to reject bad samples (e.g. that resulted from an unfortunate random draw) on its own. This is troublesome, however, since it is not clear a priori what a “high” probability is, and accordingly what kind of score one should strive for. This is particularly true in the (common) case where the data is treated as continuous, and the probabilities computed are actually densities. Also, this approach seems inappropriate for judging novelty – truly novel work would likely receive a low probability and thus be difficult to differentiate from work that is simply low-quality, which would also receive a low score.

Additionally, none of these models use their “self-judging” abilities to actually iterate and improve on their own outputs. This is fairly common in a creative process: Create something (perhaps only partially), judge which parts are good/bad and improve on the ones that are lacking. Here, I find self-attention approaches such as the transformer interesting: The model can essentially take multiple turns in creating something, looking at specific parts of its own output and use this information to iterate further. However, current transformer models usually do not produce actual outputs (in data space) at each layer; instead they compute on high-dimensional hidden representations and only produce an output at the very end.

Given our evolutionary history, I believe it’s safe to say that perception came first, and the ability and desire for creativity arose out of these capacities. At the same time, generative and perceptual processes could also be tightly interlinked inside a model, e.g. using a predictive coding framework. At this time, I don’t know enough about PC to really make a judgement (or go into more detail), however.

Intentionality

Likely the biggest challenge in modeling (human) creativity is that art is usually “about” something, meaning that it relates in some way to the artist’s own experience in the world. As such, properly approaching this subject seems to require solving strong AI. However, there may be ways to at least make steps towards a solution via simpler methods. One example could be multi-modal representations. As humans, we are able to connect and interrelate perceptions from different senses, e.g. vision, touch and hearing. We can also relate these perceptions to memories, abstract concepts, language etc. It seems obvious that such connections inform many creative artifacts. For example, program music provides a “soundtrack” that fits a story or series of events. Such music is neither creatable nor understandable without understanding language/stories (which in turn requires general world knowledge). On a more personal level, an artist may create a piece of music that somehow mirrors a specific experience, say, “lying at night at the shore of a calm mountain lake”.

Models that simply learn to approximate a given data distribution (limited to the modality of interest) clearly cannot make such connections.⁶ However, this could be different for a model that learns about audio and vision (for example) concurrently. As long as there is some connection between modalities, e.g. via a shared conceptual space (embeddings are an extremely popular method and could be a simple way of achieving this to a first approximation) it should be possible for the model to connect the visual concepts it is learning about with the audio dimension. This, like the other proposals in this text, is obviously an extremely rough sketch with many, many details to be considered – but this requires research, not blog posts.

Conclusion

To summarize:

• Existing deep generative models mainly aim to copy a given data distribution. This condemns them to produce artifacts that are “like” the training data in that they simply follow learned statistical regularities. Data-free models could instead have the potential to discover truly “new” artifacts from more general principles.
• Existing models learn a fixed distribution and generally do not evolve beyond this, making them “uncreative” by design. Methods from open-endedness research could result in models that continually push the boundaries of their own creations.
• Symbolic models are too far removed from the modality of interest (audio) to be meaningful on their own. Pure waveform models ignore important inductive biases from how music and sound are created. Hybrid models seem the most promising, but there are obstacles regarding their implementation and training with current methods.
• Perception, or the ability for appreciation, is an important aspect of creativity that is lacking in current models.
• Intentionality is central to art and creativity, but is missing from current models; nor is it possible to achieve by modeling data distributions in a single modality.

Each of these points offers several directions for future research to explore. It is possible that none of these proposed methods/directions will result in anything comparable to copy models, in terms of surface-level quality, for a very long time. However, I believe it is important to break the mould of trying to make progress by throwing humongous amounts of compute at highly complex data distributions. Instead, generative music (at least for creative purposes) should start from first principles and accept that the results might be “lame” for a while. In the long term, this has the potential to teach us about music, about creativity in general, and about ourselves. Can Jukebox do that?

About Delft

Here are some facts I learned about the city:

• It rains a lot, but apparently only while people are asleep. How considerate!
• Pedestrians are at the bottom of the food chain. What are sidewalks?
• …that’s pretty much it. We didn’t really get a chance to see the city amidst all the conferencing. The historical city center is very beautiful though!

Tutorials

The first day of the conference mainly consisted of two tutorial sessions. There were three topics for each slot, so you had to pick one. Since I was there with Sebastian, we decided to split up and each visit different topics. Instead of discussing the tutorials themselves, however, I would like to discuss my personal takeaways as to how you (IMHO) should structure such a session (and what you should avoid).

1. Know your audience. You cannot please everyone; if you try, you will most likely please noone. What will probably happen that your “middle ground” compromise is still too much/overwhelming for novices, while experts in the topic will be bored. Instead, I believe you should focus on one of the two groups (or on a group somewhere inbetween – but be specific).
   Now, you might say that it is impossible to know your audience at such an event – there’s too much diversity in people’s background! This just needs a slight readjustment, however: You can determine your audience instead. E.g. if you offer a GAN-for-Music tutorial advertised at people already familiar with the basics of GANs, then you can assume that the people in your tutorial fulfill those requirements. People who don’t will likely go to a different tutorial. This isn’t ideal in terms of inclusiveness, of course, but I believe it would lead to much more “useful” sessions overall.
2. Foster activity/interaction. This depends somewhat on the length of the session: IMHO, the longer it is, the more important it becomes that you do something at some point. The big thing here is that running pre-made IPython notebooks doesn’t qualify. Rather, you should include activities that really force the participants to actively engage with the material. If these activities also involve cooperation between participants, this will also allow give people an excuse to get to know their peers a little. This is particularly relevant if tutorials are in the beginning of (or before) the “main” conference.
   Generally, including interactive sessions will result in not covering as much ground, but I believe this is worth it if it means that you do so much more thoroughly. It should also make your tutorial “stick” more, which I believe is the most important thing – you can’t cover a lot of content in two or three hours anyway.

Highlight Papers

These aren’t necessarily the “best papers”, but colored by my own preferences or things I just found “cool”. Note that the order in this post is simply the order in which the papers were presented.

mirdata

The paper by Bittner et al. is an interesting case of “meta research”, showing the phenomenon of different people working with differing version of the “same” dataset, as well as the significant impact this can have on the results. While they only sample a small number of exemplary datasets, it makes you wonder how many research projects are/were affected by problems like this.

The authors also propose a Python library for unified distribution and verification of MIR datasets. This is great, if only for the fact that datasets that do not come from the same source often come in different formats requiring separate preprocessing procedures etc. A common repository can reduce the load of having to write new processing code for each new dataset.

Informational Complexity in Music

This paper by Parmer et al. investigates the “complexity” in terms of information theory of various western music styles and its development over time. While the methodology can be questioned – e.g. the information measure is limited and not verified with regard to human perception of complexity – there are some interesting findings about how different genres seem to “prioritize” different areas of complexity, how the different areas developed over time, and how Billboard Top 100 songs differ (or don’t) from the general population of songs.

Unsupervised Drum Transcription

Choi et al. tackle the problem of unsupervised transcription in this paper, based on how a human might do it: Listen to a piece of music, try to play it, and adjust your play to fix any errors on your part (i.e. differences between what you heard and what you played).

The core idea is to use an encoder-decoder approach with a fixed decoder (your “instrument”). By limiting the decoder to essentially produce impulse responses for certain instruments, the encoder is forced to produce the corresponding transcriptions. This of course has many limitations, e.g. a limited set of “sounds” the decoder can produce, as well as the decoder needing to be differentiable. Making this approach work for non-drum sounds would probably need a lot of extra work, but in my opinion it’s still a cool idea.
Another interesting thing is their use of the sparsemax activation, which I didn’t know about before – a kind of sparse (but differentiable) alternative to softmax.

A special shoutout goes to their training dataset, which apparently “was crawled from various websites”. Way to foster reproducibility!

Transcription with Invertible Neural Networks

Invertible neural networks are, essentially, able to map back from their output to the input. Kelz et al. introduce this concept to MIR tasks in their paper. The networks are very close to flow-based generative models, but there is the problem that in classification tasks, we usually don’t want the output to carry all information in the input (or even be the same size as the input), which makes inverting the network rather difficult. To fix this issue, there is an “auxiliary” output that carries the extra information needed for invertibility, but not for the actual task of interest.

Invertible neural networks primarily promise better interpretability of trained models, which is definitely needed in deep learning. For example, in the case of transcription, a given symbolic (transcribed) piece of music can be inverted to give an example sound that would be transcribed this way. This way, one can check whether the concepts that the model learned make sense intuitively. As an added bonus, we get a generative model “for free” by training a discriminative one.

Resonance Equalization with Neural Networks

Grachten et al. propose a kind of “neural equalizer” that automatically attenuates resonances in music. They show that a network working directly on raw audio performs on par with hand-crafted feature pipelines. I suppose this isn’t super impressive to most people, but I like the idea of incorporating AI/ML into music production. Possible future work includes processing a piece of music such that it adheres to some desired spectral profile (i.e., which frequencies should be present how strongly?). Check the paper.

AIST Dance Video Database

Not my topic at all, but this dataset represents a huge effort: Thousands of videos, 40 dancers, several genres, up to nine cameras… Plus, it’s all free and open. Cheers to Tsuchida et al.!

Google Scooped My Idea

The folks at Google Magenta presented a paper on efficient neural audio synthesis. What I find more relevant is the follow-up, currently under review for ICLR, which is basically what I wanted to do to kick off my PhD. Oh well. Check it out though, the examples are quite impressive. And yet, lots of work still to be done…

FMP Notebooks

Müller et al. probably didn’t “need” to write this paper since the notebooks kind of stand on their own, but I suppose it is rather like a “companion paper” since, unfortunately, papers are still the most important thing in research. Read the paper, check out the notebooks, read the FMP book… it’s all good stuff.

Invariance Through Complex Basis Functions

At a glance, the paper by Lattner et al. is a bit too complex for me (hahaha), but this is definitely something I’ll be playing around with in the near future in order to gain some understanding. The idea is to learn invariances to several “simple” kinds of transformations such as transposition or time-shifting, although the authors also demonstrate uses in the image domain (e.g. rotation). Unfortunately, the paper leaves out most ofthe visualizations of the learned filters that were on the poster, which looked really intriguing.

Mosaic Style Transfer with Autocorrelograms

This paper by MacKinlay et al. sounded super cool (and he was really nice to talk to at the poster!), but I have to admit that this goes way over my head mathematically. Another one I’m going to have to do some tinkering with. :) Unfortunately they don’t include sound examples in the paper, but it provides a method doing “musical style transfer” (i.e. transfering the timbre of one signal onto the melody of another). While this isn’t “new” per se, the approach sounds quite sensible, plus it’s IMHO more attractive than just “letting a neural network do it”, which most style transfer solutions nowadays seem to go for.

Late-breaking Demos

The LBD session was for “experimental” stuff that wasn’t ready in time for the regular deadline; it was also “just” posters (and optional demos), no papers. Unfortunately, there was very little time given the sheer amount of stuff, so here are just some quick highlights:

• The guys from this paper seemed to have finished their “intuitively controllable” synthesizer. Not sure when/if/where they’re going to release it though…
• Apparently, differentiable synthesizers are getting more popular right now: Hirata et al. tested “deep frequency modulation synthesis”. Looks like this was already published at CMMR, so I’m not sure why it was in the session, and it looks like it needs a lot of work, but I thought it was cool.
• There was a poster on cross-fading between two audio tracks in the time-frequency domain, i.e. cross-fade different frequencies at different times. Unfortunately I don’t have a link!

Unconference

There was an “unconference” session with some interesting topics. Unfortunately, it overlapped with the LBD session, so I ended up not going… Shame, the whole conference was set up in a “single-track” way, but it seems like they just wanted to do a bit too much on Friday, so this kinda fell under the wagon. Maybe next year!

In Closing

A few more general takeaways:

• Deep Learning is taking over MIR (of course…), but the methodology seems to be rather simple still. I.e. the models used are often fairly “vanilla” and there is little in terms of interpretability/understanding what’s going on inside. I suppose this will become more relevant once the models really start saturating on the main MIR tasks and progress will require new approaches. I feel like a kind of meta-review on the state of DL in MIR could be useful.
• Please don’t read your one-hour keynote presentation in the evening. Bad combination.
• Five days is a bit much for me. Around the fourth day or so, I really felt my mental capacities decreasing, and crowding around posters for hours a day became really exhausting. For people for whom this is an issue, it might be necessary to plan your visit a bit more, e.g. not going to all the events on the first days to conserve your energy.

Overall, ISMIR 2019 was a great time! Met plenty of nice people, ate some great food, got lots of new input… And motivation to submit something to next one so we can go to Montreal next year. :) See you there!

This tutorial is based on one that was previously found on the Tensorflow website. You can check that one for additional conceptual guidance, however the code snippets found there are intended for old Tensorflow versions (1.x). Since the official TF website is now lacking a comparable tutorial (the simple MNIST tutorials use Keras instead of low-level concepts), the following is supposed to offer an updated version working in Tensorflow 2.0. It is intended as a supplementary tutorial for Assignment 1 of our Deep Learning class and assumes that you already went through the other posts linked there.

Walkthrough

Preparation

Download this simple dataset class and put it in the same folder as your script/notebook. It’s just a wrapper for simple production of random minibatches of data.

Imports

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from datasets import MNISTDataset

Loading data and sanity checking

We make use of the “built-in” MNIST data in Tensorflow. We plot the first training image just so we know what we’re dealing with – it should be a 5. Feel free to plot more images (and print the corresponding labels) to get to know the data! Next, we create a dataset via our simple wrapper, using a batch size of 128. Be aware that the data is originally represented as uint8 in the range [0, 255] but MNISTDataset converts it to float32 in [0,1] by default. Also, labels are converted from uint8 to int32.

mnist = tf.keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

plt.imshow(train_images[0], cmap="Greys_r")

data = MNISTDataset(train_images.reshape([-1, 784]), train_labels, 
                    test_images.reshape([-1, 784]), test_labels,
                    batch_size=128)

Setting up for training

We decide on the number of training steps and the learning rate, and set up our weights to be trained with random initial values (and zero biases).

train_steps = 1000
learning_rate = 0.1

W = tf.Variable(np.zeros([784, 10]).astype(np.float32))
b = tf.Variable(np.zeros(10, dtype=np.float32))

Training

The main training loop, using cross-entropy as a loss function. We regularly print the current loss and accuracy to check progress.

Note that we compute the “logits”, which is the common name for pre-softmax values. They can be interpreted as log unnormalized probabilities and represent a “score” for each class.

In computing the accuracy, notice that we have to fiddle around with dtypes quite a bit – this is unfortunately common in Tensorflow.

for step in range(train_steps):
    image_batch, label_batch = data.next_batch()
    with tf.GradientTape() as tape:
        logits = tf.matmul(image_batch, W) + b
        loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
            logits=logits, labels=label_batch))
        
    gradients = tape.gradient(loss, [W, b])
    W.assign_sub(learning_rate * gradients[0])
    b.assign_sub(learning_rate * gradients[1])
    
    if not step % 100:
        predictions = tf.argmax(logits, axis=1, output_type=tf.int32)
        acc = tf.reduce_mean(tf.cast(tf.equal(predictions, label_batch),
                             tf.float32))
        print("Loss: {} Accuracy: {}".format(loss, acc))

Predicting/testing

We can use the trained model to predict labels on the test set and check the model’s accuracy. You should get around 0.9 (90%) here.

test_predictions = tf.argmax(tf.matmul(data.test_data, W) + b, axis=1,
                       output_type=tf.int32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(test_predictions, data.test_labels),
                             tf.float32))
print(accuracy)

The release of Tensorflow 2.0 is supposedly around the corner (at the time of writing, the current version is rc0), and with it comes the promise of a more streamlined and intuitive API through things like full Keras integration and eager execution. However, new ways of doing things also bring new problems. In this post, I want to summarize some common issues along with ways to avoid or fix them. Most of these come from own experience or questions on Stackoverflow. It is intended mostly as a compendium for new users and people taking our classes, but perhaps others can profit as well. Note that I might update this post in the future if more things come up (or there might be a part 2 instead)!

tf.function

tf.function promises to make the switch between eager and graph mode easy – develop, prototype and debug in eager execution and then slap on this decorator for production-level performance. That’s the idea – in practice, there are so many quirks with this thing that one could write a whole series of posts on this alone – and in fact people have done so already. That link points to a three-part post discussing this topic at length. I highly recommend reading it in detail, but I want to include some “highlights” here:

Function arguments: Tensors vs Python types

To understand this issue, note what a tf.function-decorated function actually does under the hood: The first time it is called, it is compiled into a graph, and then any other time the function will simply execute the graph instead – the Python function is basically “ignored”. Consider this simple example:

@tf.function
def fun():
    print("hello")

fun()
fun()

>>>hello

As we can see, the print statement is only executed once even though we called the function twice – it doesn’t make it into the compiled function.

This is, however, not the full story: Actually, the function is compiled once for each input signature instead. This has dramatic implications if the function accepts Python numeric types, where each new value actually leads to a new input signature!! If this sounds a bit complicated, just consider the following example:

import time

@tf.function
def fun(x, step):
    return 5*x

start = time.time()
for step in range(1000):
    dummy_fun(0, step)
stop = time.time()

print(stop-start)

>>>12.037055969238281

The function is compiled anew every time it is called with a new step count (which is every time we call it)! This will slow down execution dramatically. Luckily, the fix is simple: Use tensors for such “changing values” instead, where different values do not count for a new input signature.

start = time.time()
for step in tf.range(1000):
    dummy_fun(0, step)
stop = time.time()

print(stop-start)

>>>0.40102267265319824

So, whenever your decorated functions are conspicuously slow (especially if they become slower after adding the decorator), you might want to check your input parameters for Python numbers! Note that this is a fairly common scenario as we may use step counters to control stuff like learning rate decay, saving a model regularly etc.¹

GradientTape

Gradient tapes are a new kind of abstraction in TF 2.0. They basically replace tf.gradient. The idea is: With eager execution, there is no static computational graph, meaning no way to trace computations and thus no way to do backpropagation. Gradient tapes offer a way to temporarily trace computations as needed so that we can still use TF’s symbolic differentiation capabilities (it would be pretty useless otherwise!). Once again, however, it’s easy to run into problems…

Collecting variables before they exist

In TF 1.x, there is the concept of collections that globally keep track of things like trainable variables. In TF 2.0, this doesn’t exist anymore: You need to keep track of your variables yourself. Often, you will do this via tf.keras.Model instances, which have a convenient trainable_variables property. Consider this:

model = tf.keras.Sequential([tf.keras.layers.Dense(10)])
var_list = model.trainable_variables

>>>ValueError: Weights for model sequential_1 have not yet been created. Weights
>>>are created when the Model is first called on inputs or `build()` is called 
>>>with an `input_shape`.

Whoops! The model was never built, so there are no variables. In the current version this leads to a crash, but older pre-releases actually executed perfectly fine – but model.trainable_variables would be empty! This would mean that your fancy training loop just went through computing gradients for and updating no variables at all… Thus, make sure you only ever use variable stores of your fully-built models:

model = tf.keras.Sequential([tf.keras.layers.Dense(10)])
model.build((None, 784))  # for MNIST ;)
var_list = model.trainable_variables

Alternatively, always using model.trainable_variables explicitly (instead of a shortcut assignment like above) can also prevent mistakes, but it can be cumbersome in some situations.

Optimizing things that are not variables

A common question is this: I want to find gradients with respect to the input to my network, e.g. to find how sensitive the predictions are to certain parts of the input, with the network itself staying fixed. I tried this but it doesn’t work:

input_ = ...  # just get a tensor from somewhere
model = ...  # same for the model

with tf.GradientTape() as tape:
    # let's say we are interested in the class with index 7
    logits_seven = model(input_)[:, 7]
grad_for_inp = tape.gradient(logits_seven, input_)

print(grad_for_inp)

>>>None

The issue lies with what kind of computations GradientTape actually traces: By default, it will store all computations related to any tf.Variable it comes across, and nothing else. In particular, since your network input is usually just a Tensor and not stored in a variable, related computations are not traced and so no gradients can be computed.² Once again, the fix is actually really simple: You need to tell the tape what to trace (or “watch”)!

with tf.GradientTape(watch_accessed_variables=False) as tape:
    tape.watch(input_)
    logits_seven = model(input_)[:, 7]
grad_for_inp = tape.gradient(logits_seven, input_)

print(grad_for_inp)

>>>tf.Tensor(
>>>[[[[ 0.03662432 -0.0254075   0.06999005]
>>>   [ 0.00372662 -0.0231829   0.01369272]
>>>   [-0.06823001 -0.0217168  -0.02034823]
>>>   ...

Note that I passed an extra parameter to tell the tape not to trace the variables it comes across (i.e. all the model parameters). This isn’t necessary for correctness, but should make the whole thing a little more efficient.

Doing “computations” outside the tape context

Here’s the example from above again:

with tf.GradientTape() as tape:
    tape.watch(input_)
    logits = model(input_)
grad_for_eight = tape.gradient(logits[:, 7], input_)

print(grad_for_eight)

>>>None

It broke again! What happened? Note that this time, I do the indexing into the “interesting” class outside of the gradient tape context. This means that the tape basically loses track of where this tensor came from and cannot compute the gradients anymore. As a rule of thumb, anything you put into tape.gradient should come straight out of the tape context without any modifications! Another common example would be when you have multiple losses (e.g. classification and regularization losses) and add them to a “total loss” outside the tape context. This won’t work!

Keras

Keras is “the” high-level interface in TF 2.0, and it is arguably much more convenient than the cumbersome Estimator interface or chaining tf.layers. But once again, it does not come without pitfalls…

Choosing the wrong variables to optimize

If using batch normalization, you might get strange warnings like this one:

>>>W0924 09:53:23.799460 140659773245184 optimizer_v2.py:979] Gradients d does not 
>>>exist for variables ['batch_normalization_1/moving_mean:0', 
>>>'batch_normalization_1/moving_variance:0'] when minimizing the loss.

Looking at the code, it may well include something like this:

grads = tape.gradient(xent, model.variables)
optimizer.apply_gradients(zip(grads, model.variables))

This can be subtle: We are using model.variables instead of trainable_variables. These are different! variables stores anything that has a “state” that needs to be stored over the course of time. In the case of batchnorm, this includes the “population statistics” batchnorm uses during inference (instead of minibatch statistics). These are not used during training and so no gradients can be computed (and you wouldn’t want this anyway!).

There are of course other cases besides batchnorm, but the root cause is often the same: You are including variables in your optimization procedure that have no business of being there. Often, using model.trainable_variables can fix this.

Using numpy where you shouldn’t

Keras models have functionality that allows us to easily execute the full model in a single line. How about this (re-using an example from above)?

with tf.GradientTape(watch_accessed_variables=False) as tape:
    tape.watch(input_)
    logits_seven = model.predict(input_)[:, 7]
grad_for_inp = tape.gradient(logits_seven, input_)

print(grad_for_inp)

>>>AttributeError: 'numpy.dtype' object has no attribute 'is_floating'

Why does this fail? All we wanted to do was the forward pass of the model. It turns out that model.predict returns a numpy array, and this quite literally interrupts the “tensor flow”, meaning no gradients can be computed either.³ Instead, make sure to always use Keras models as callables as in the examples above. This still holds if you try to be smart and “just go back to Tensorflow” again:

with tf.GradientTape(watch_accessed_variables=False) as tape:
    tape.watch(input_)
    logits_seven = model.predict(input_)[:, 7]
    logits = tf.convert_to_tensor(logits)
grad_for_inp = tape.gradient(logits_seven, input_)

print(grad_for_inp)

>>>None

Do note that this applies to anything involving numpy arrays – gradients cannot propagate through these operations!! This has always been the case, but is arguably a bigger problem in TF 2.0 where it is so tempting to mix between eager execution and numpy arrays.